Elements Of Statistical Learning, Part 1

Contents:

Chapter 1: Introduction

Variable types and terminology
- Quantitative vs Qualitative output.
- Regression and Classification
Simple approaches : Least Squares and Nearest Neighbors
- Linear Models and Least Squares
  \(\hat Y = \hat \beta_0 + \sum_{j=1}^pX_j\hat\beta_j\)
  - Least squares by solving normal equations.
- Nearest Neighbor Methods
  - Voronoi tessellation
- From Least Squares to Nearest Neighbors
Statistical Decision Theory
Local Methods in High Dimensions
- The curse of Dimensionality,Bellman
Statistical Models, Supervised Learning and Function Approximation
- A Statistical Model for the Joint Distribution Pr(X, Y )
- Supervised Learning
- Function Approximation
Structured Regression Models
- Difficulty of the Problem
Classes of Restricted Estimators
- Roughness Penalty and Bayesian Methods
  - regularization
- Kernel Methods and Local Regression
- Basis Functions and Dictionary Methods
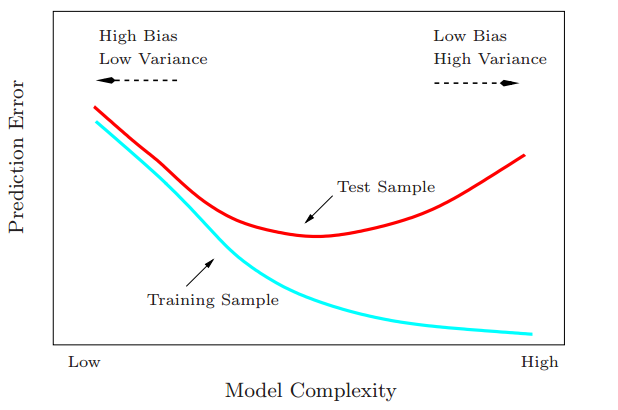
Model Selection and the Bias–Variance Tradeoff

Introduction
Linear Regression Models and Least Squares
- Solution from normal form
- F statistic
- Example : prostrate cancer
- The Gauss-Markov Theorem
  - Proof that the Least Squares estimate for the parameters, \(\beta\) has the least variance.
- Multiple Regression from Simple Univariate Regression
- Multiple Outputs
Subset Selection
- Best-Subset Selection
- Forward and Backward-Stepwise Selection
- Forward-Stagewise Selection
- Example : Prostrate Cancer (Continued)
Shrinkage Methods
- Ridge Regression : L2 regularization
- The Lasso : L1 regularization
- Discussion : Subset Selection, Ridge Regression and the Lasso
- Least Angle Regression
Methods Using Derived Input Directions
- Principal Components Regression
- Partial Least Squares
Discussion : A Comparison of Selection and Shrinkage Methods
Multiple Outcomes Shrinkage and Selection ☠
More on Lasso and Related Path Algorithms ☠
- Incremental Forward Stagewise Regression
- Piecewise-Linear Path Algorithms
- The Dantzig selector
- The Grouped Lasso
- Further Properties of Lasso
- Pathwise Coordinate Optimization
Computational Considerations
- Fitting is usually done using Cholesky decomposition of matrix \(X^TX\).

Introduction
Linear Regression of an Indicator Matrix
Linear Discriminant Analysis
- Regularized Discriminant Analysis
- Computations for LDA
- Reduced-Rank Linear Discriminant Analysis
Logistic Regression
- Fitting Logistic Regression Models
- Example : South African Heart Disease
- Quadratic Approximations and Inference
- \(L_1\) Regularized Logistic Regression
- Logistic Regression or LDA ?
Separating Hyperplanes
- Rosenblatt’s Perceptron Learning Algorithm
- Optimal Separating Hyperplanes ☠

Introduction
Piecewise Polynomials and Splines
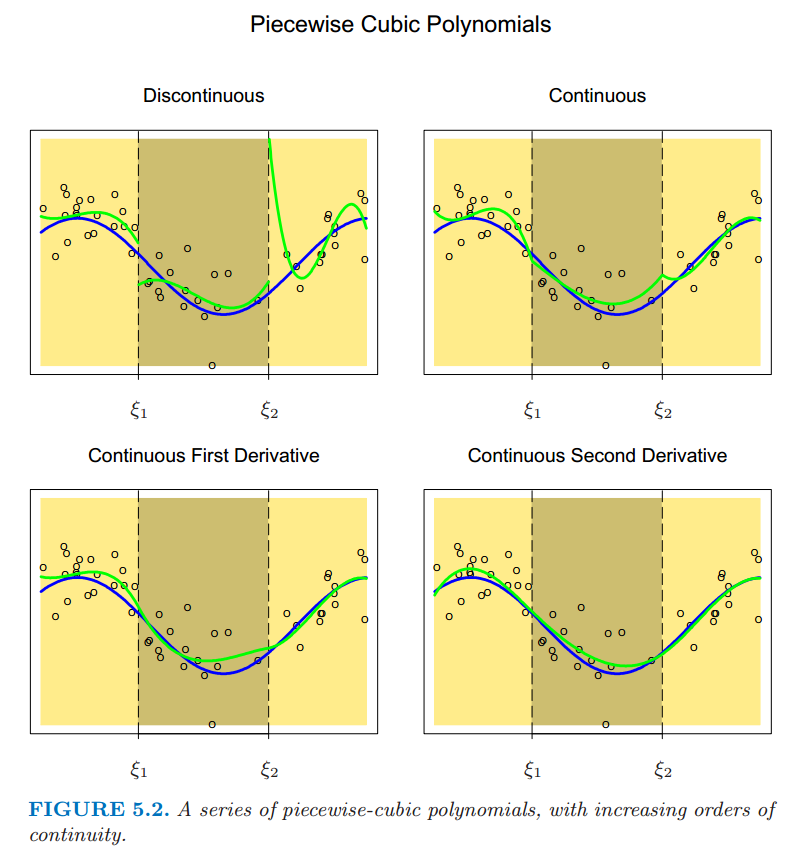
- Natural Cubic Splines
- Example: South African Heart Disease (Continued)
- Example: Phoneme Recognition
Filtering and Feature Extraction
Smoothing Splines
- Degrees of Freedom and Smoother Matrices
Automatic Selection of the Smoothing Parameters
- Fixing the Degrees of Freedom
- The Bias–Variance Tradeoff
Nonparametric Logistic Regression
Multidimensional Splines
Regularization and Reproducing Kernel Hilbert Spaces ☠
- Spaces of Functions Generated by Kernels
- Examples of RKHS
- Penalized Polynomial Regression
  - Gaussian Radial Basis Functions
  - Support Vector Classifiers
Wavelet Smoothing ☠
- Wavelet Smoothing and the Wavelet Transform
- Adaptive Wavelet Filtering

One-Dimensional Kernel Smoothers
- Local Linear Regression
- Local Polynomial Regression
Selecting the Width of the Kernel
Local Regression in \({\mathbb R}^p\)
Structured Local Regression Models in \({\mathbb R}^p\)
- Structured Kernels
- Structured Regression Functions
Kernel Density Estimation and Classification
- Kernel Density Estimation
- Kernel Density Classification
- The Naive Bayes Classifier
Radial Basis Functions and Kernels
Mixture Models for Density Estimation and Classification
Computational Considerations