Contents:
Chapter 0: Prologue
- Books and algorithms
- Ideas that changed the world.
- Widespread use of decimal system.
- Enter Fibonacci
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ....,- Also, \(F_n = F_{n-1} + F_{n-2}\)
- And, \(F_n ≈ 2^{0.694n}\)
- A naive implementation , with no caching of values..,
fib1- Runtime --> \(T(n) >= F_n\), exponential in n
- Can We Do Better,....?
- A Polynomial algorithm...,
fib2- A loop based algorithm that remembers previous values in an array.
- Polynomial running time.
- More Careful Analysis
- What about addition of numbers Fibonacci values for large n.
- Adding two n-bit integers take time ~ n.
- So, \(fib1 ≈ n.Fn\)
- And, \(fib2 ≈ n^2\)
- Big-O notation
- Right simplification of the analysis.
- Leave behind the lower order terms.
- General rules :
- Multiplicative constants can be omitted.
- \(n^a\) dominates \(n^b, if a > b\)
- Any exponential dominates any polynomial. \(a^n\) dominates \(n^b\)
- Likewise, any polynomial dominates any logarithm. \(n\) dominates \(log(n)\)
- Exercise 0.4
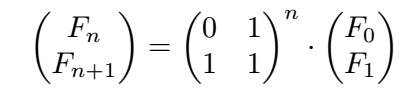
- So now \(F_n\) can be computed by calculating \(X^n\) where \(X\) is the square matrix.
- So, \(Fn = O(log n)\)
- But then, with careful analysis,
- Multiplication of large n-bit numbers \(≈ O(n^2)\)
Chapter 1: Algorithms with Numbers
Two ancient problems:
Factoring : Given a number N, express it as a product of its prime factors. Hard
Primality : Given a number N, determine whether it is a prime. Easy
Basic Arithmetic

- Addition
The sum of any three single-digit numbers is at most two digits long.
Given two binary numbers x and y, how does our algorithm take to add them?
Depends on size of input, number of bits in x and y.
Running time \(= O(n), n =\) number of bits in the numbers.
Is there anything faster? No..
About word length and large numbers -
Multiplication and Division
To multiplyxandy, create an array of intermediate sums, each representing the product ofxby a single digit ify. These values are appropriately left shifted and added up.-
Running time = Addition of n numbers of n-bits length = \((n-1).O(n)\) = \(O(n^2)\)
-
Another fascinating algorithm for multiplication:


However, running time = \(O(n^2)\) , n = number of bits.

-
Modular Arithmetic
- Modular arithmetic is a system for dealing with restricted ranges of integers.
-
Another interpretation is that modular arithmetic deals with all the integers, but divides into N equivalence classes, each of the form \(\{i+kN:k\in \mathbb Z\}, i \in [0, N-1]\).
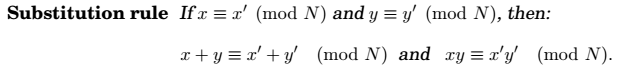

-
Modular addition and multiplication
Toaddtwo numbers x and y modulo N, we start with regular addition. Since x and y are both in the range 0 to N - 1, their sum is in the range 0 to 2(N-1). If the sum exceeds N-1, we merely need to subtract off N to bring it back to required range. So, running time \(= O(n), n = log N\).To
multiplytwo mod N numbers x and y, do regular multiplication, reduce the answer to modulo N. The product can be as large as \((N-1)^2\), at most 2n bits large. Need to compute the remainder using quadratic time division algorithm. Multiplication thus remains quadratic.Division, however is tricky, whenever legal, it can be managed in quadratic time. -
Modular exponentiation
We want to compute \(x^y \pmod N\).

Let n be the size(bits) of x, y and N. As with multiplication, the algorithm will halt after at most n recursive calls, and during each call it multiplies n-bit numbers, for a total running time of \(O(n^3)\). -
Euclid's algorithm for G.C.D

Eculid's rule : If x and y are positive integers with \(x >= y\) , then \(gcd(x, y) = gcd(x \pmod y, y)\).
Also, if \(a > b\), then \(a \pmod b < a/2\).
This means after any two consecutive iterations, both arguments are at the very least reduced to half.If they are initially n-bit, base case will be reached in at most 2n recursive calls. And each call involves a quadratic-time division. Running time \(= O(n^3)\). -
An extension to Euclid's algorithm A small extension to Euclid's algorithm is the key to dividing in the modular world.

- Modular division
x is the multiplicative inverse of a modulo N, if \(ax == 1 \pmod N\)
If \(gcd(a,N) > 1 , \Rightarrow ax \neq 1 \pmod N \forall x\), and therefor a cannot have a multiplicative inverse modulo N.
When \(gcd(a, N) = 1\), we say a and N are relatively prime.
The extended Euclid's algorithm gives us integers x and y such that \(ax + Ny = 1\), which means \(ax \equiv 1 (mod N)\) . Thus x is a's sought inverse.
Modular Division Theorem , a has multiplicative inverse modulo N, if and only if they are relatively prime, and it can be found by running extended Euclid theorem in time \(O(n^3)\).

- Primality Testing
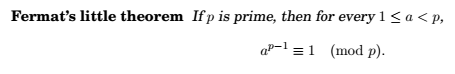

Here the theorem does not say anything about what happens if number is not prime.
In fact, for some composite numbers, Pr(Algorithm returns yes when N is not prime) <= 1/2 We can thus choose k different random integers to test for primality testing, reducing Pr to \(1/2^k\).- Generating random primes

Due to such abundance of prime numbers, prime number generation is easy.- Generate a random n-bit number.
- Check for primality.
- If not prime, repeat the process.
- Generating random primes
Cryptography
Rivest-Shamir-Adelman(RSA) : Blabber about private key and public key systems.
- Private-key schemes: one time pad and AES
- RSA
Public key cryptography
Based heavily upon number theory.

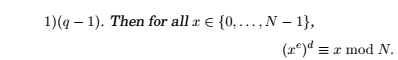

Universal Hashing
- Hash Tables
Give a
keyto anyvalue.
Hash function : How to define the mapping betweenkeyandvalue. - Families of Hash Functions

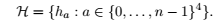
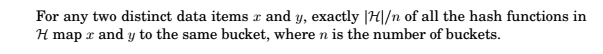
A family of hash functions with this property is called universal .
Comments
comments powered by Disqus