Algorithms, Part 2

Contents:

Chapter 2: Divide-and-Conquer Algorithms

The divide and conquer strategy solves a problem by
1. Breaking it into sub-problems that are themselves smaller instances of the same type of problem.
2. Recursively solving these problems.
3. Appropriately combining their results.

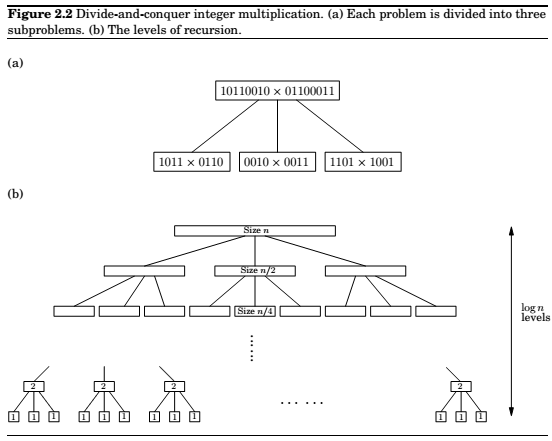
Multiplication

For multiplying two n-bit integers x and y.
\(x = \bbox[5px, border:2px solid black]{ x_L } \quad \bbox[5px, border:2px solid black]{ x_R } = 2^{n/2}x_L + x_R\)
\(y = \bbox[5px, border:2px solid black]{ y_L } \quad \bbox[5px, border:2px solid black]{ y_R } = 2^{n/2}y_L + y_R\)

then, \(xy = (2^{n/2}x_L + x_R)(2^{n/2}y_L + y_R) = 2^nx_Ly_L + 2^{n/2}(x_Ly_R + x_Ry_L) + x_Ry_R\)

Now, we can compute xy by evaluating the RHS. Addition and multiplication by \(2^n\) are linear time. Rest of the 4 multiplications can be done by recursively applying this algorithm.

So, \(T(n) = 4T(n/2) + O(n)\).

Which results in \(O(n^2)\).

By expanding the middle term, we can do with just three calculations, \(x_Ly_L , x_Ry_R, (x_L+x_R)(y_L+y_R)\).
since,
\(x_Ly_R + x_Ry_L = (x_L + x_R ) (y_L + y_R ) - x_Ly_L – x_Ry_R\).

Resulting algorithm would then be
\(T(n) = 3T(n/2) + O(n)\), which is \(O(n^{1.59})\)

Height of the tree \(= \log_2 n\), since the length of the sub-problem gets halved at every level.
Branching factor = 3.

So, at any level k we will have \(3^k\) to solve each of size \(n/2^k\).

Therefore, time spent at level k is, \(3^k \times O(\frac n {2^k}) = (\frac 3 2)^k \times O(n)\)

Which is a geometric series. So, the sum then approximates to the last term of the series.
That is \(O(3^{\log_2 n})\), which can be written as \(O(n^{\log_2 3})\), which is about \(O(n^{1.59})\).

Can we do better ??? using Fast Fourier Transforms discussed later.

Recurrence relations

Consider this recurrence tree.

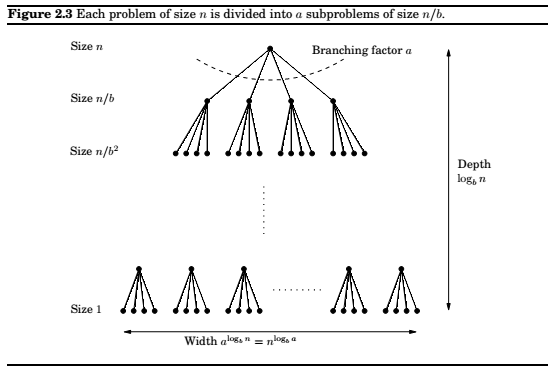
Master's Theorem :
If \(T(n) = aT(\lceil n/b \rceil) + O(n^d)\) for some constants \(a > 0, b > 1\), and \(d \ge 0\), then

$$ T(n) = \begin{cases} O(n^d), \text{ if } d > \log_b a \\ O(n^d\log n), \text{ if } d = \log_b a \\ O(n^{\log_b a}), \text{ if } d < \log_b a \end{cases}$$

Mergesort

Sort an array by recursively sorting each half and merging the results.

Since merge does constant amount of work per recursive call, overall time is

$$ T(n) = 2T(n/2) + O(n), \text{ or } O(n\log n)$$


Here is an iterative version using a Queue.

Medians

Median = 50th percentile of a list of numbers.

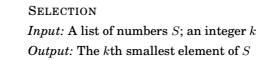
A randomized divide-and-conquer algorithm for selection
For any number v, Split S into three categories: elements smaller than v \((S_L)\), equal to v \((S_v)\) , greater than v \((S_R)\) , then

$$ selection(S, k) = \begin{cases} selection(S_L, k), \quad\quad\quad\quad\quad\quad \text{if } k \le |S_L| \\ v , \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \text{ if } |S_L| < k \le |S_L| + |S_v| \\ selection(S_R, k - |S_L| - |S_v|), \text{ if } k > |S_L| + |S_v| \end{cases}$$

The three sub-lists can be computed in linear time, even in place.
How to pick v ? Randomly from S.

Matrix multiplication


Symbolically,

$$ Z_{ij} = \sum_{k=1}^n X_{ik}Y_{kj}$$

This implies the algorithm to be \(O(n^3)\)

Enter divide-and-conquer.
Divide the matrices X and Y into 4 blocks.

$$ X = \begin{bmatrix} A & B \\ C & D \end{bmatrix}, Y = \begin{bmatrix}E & F \\ G & H\end{bmatrix} $$

,

Then, their product can be expressed as,

$$ XY = \begin{bmatrix}A & B \\ C & D\end{bmatrix} = \begin{bmatrix}AE+BG & AF+BH \\ CE+DG & CF+DH \end{bmatrix} $$

Total running time can be described as,
\(T(n) = 8T(n/2) + O(n^2), \text{ which is again } O(n^3)\).

Turns out you can do this,

$$ XY = \begin{bmatrix}P_5+P_4-P_2+P_6 & P_1+P_2 \\ P_3+P_4 & P_1+P_5-P_3-P_7\end{bmatrix} $$

where,
\(P_1 = A(F-H) \quad\quad P_5 = (A+D)(E+H)\)
\(P_2 = (A+B)H \quad\quad P_6 = (B-D)(G+H)\)
\(P_3 = (C+D)E \quad\quad P_7 = (A-C)(E+F)\)
\(P_4 = D(G-E)\)

The new running time is, \(T(n) = 7T(n/2) + O(n^2), \text{which is } O(n^{\log_2 7}) \approx O(n^{2.81})\)

Fast Fourier transform

Next target, Polynomials.

The general solution for polynomial multiplication works in \(\theta(d^2)\) time, where \(d\) is the degree of polynomials.

An alternative representation of polynomials.

Fact : A degree-d polynomial is uniquely characterized by its values at any \(d+1\) distinct points.

So, we can specify a degree-d polynomial

$$A(x) = a_0+a_1x+...+a_dx^d$$

by any one of the following,
1. Its coefficients, \(a_0, a_1,..., a_d\)
2. The values \(A(x_0), A(x_1), ..., A(x_d)\)

Now, taking in consideration the second form, the product has a degree \(2d\), and is completely determined by its values at \(2d+1\) points.
Since, those values are just products of the two polynomials at the given point. Thus, polynomial multiplication takes linear time in the value representation.

Evaluation by divide-and-conquer
The Trick : Choose the n points to be selected as positive-negative pairs, then the computations needed to be done overlap a lot.
Specifically,

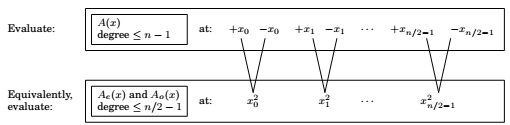
if we could then recurse, we would have,

$$T(n) = 2T(n/2) + O(n), \text{which is } O(n\log n)$$


But, recursing it at the second level and beyond seems impossible. Unless, of-course we use complex numbers.
To get positive-negative pairs at subsequent levels, we can use the roots of \(z^n = 1\)
Which are, \(1, \omega, \omega^2, ... \omega^{n-1}, \text{ where, } \omega = e^{2\pi i/n}\)

So, if we choose these numbers, at every successive level of recursion we have pairs of positive-negative numbers

Interpolation

$$\langle \text{values} \rangle = FFT(\langle \text{coefficients} \rangle, \omega)$$

, and

$$\langle \text{coefficients} \rangle = \frac 1 n FFT(\langle \text{values} \rangle, \omega^{-1}) $$

Details left,, See Fourier basis

A closer look at the fast Fourier Transform
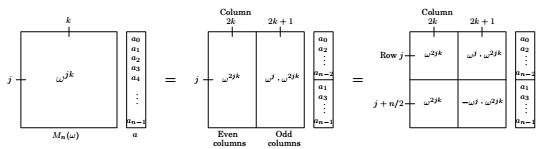
The FFT takes as input a vector \(a = (a_0, ... a_{n-1})\) and a complex number \(\omega\) whose powers are the complex root of unity.
It multiplies this vector with the Matrix \(M_n(\omega)\), which has \((j, k)_{th}\) entry (starting row and column count at zero) \(\omega^{jk}\).

Comments

comments powered by Disqus