Contents:
Combinatorial Problems
Check out Numerical Recipes
Whats different?
- Issues of Precision and Error. Floating point issues. Use both single and double precision, and think hard when they diverge.
- Extensive Libraries of Code. There is no reason to not to use all thats already written.
Sorting
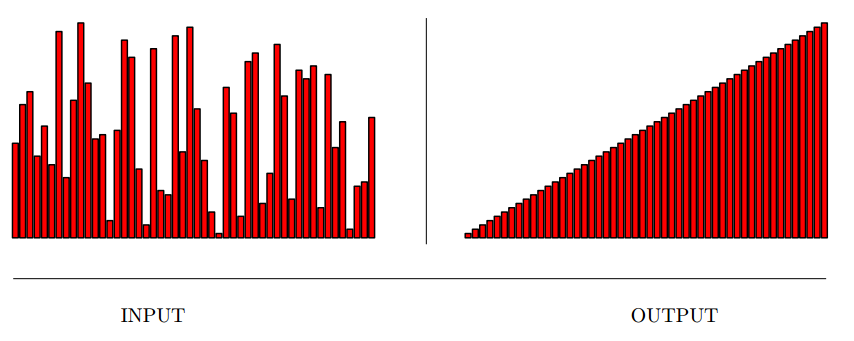
Input description: A set of \(n\) items.
Problem description: Arrange the items in increasing (or decreasing) order.
- The most fundamental algorithmic problem in computer science.
- First rule of algorithm design : "when in doubt, sort"
- Questions to ask,
- How many keys will you be sorting? Use simple routines.
- Will there be duplicate keys in the data? Do you need sort to be stable?
- What do you know about your data?
- Has the data already been partially sorted? Insertion sort would perform much better.
- Do you know the distribution of the keys? A bucket or distribution sort would make sense.
- Are your keys very long or hard to compare? It might make sense to use prefixes, or maybe use radix sort.
- Is the range of possible keys very small? Use something like counting sort.
- Do I have to worry about disk accesses? Use external sorting, or use B-tree.
- How much time do you have to write and debug your routine?
- If you want to implement your own quicksort,
- Use randomization,
- Median of three
- Leave small subarrays for insertion sort
- Do the smaller partition first. compiler optimizations using tail recursion might help.
- Implementations : GNU sort, C++ STL
sortandstable_sort, and many more. - Related : Dictionaries, searching, topological sorting
Searching
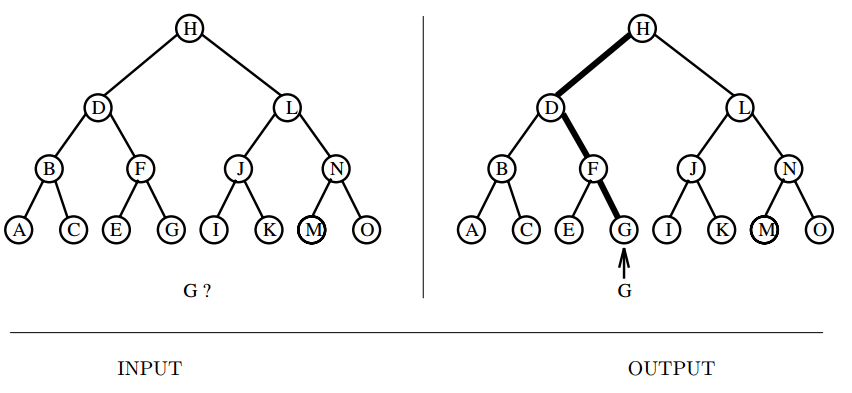
Input description: A set of \(n\) keys \(S\), and a query key \(q\).
Problem description: Where is \(q\) in \(S\)?
- "Searching" is a word that means different things to different people.
- We consider the task of searching for a key in a list, array or a tree.
- Sequential search vs. Binary search.
- Questions to ask,
- How much time can you spend programming? Binary search can be tricky to be made bug free.
- Are certain items accessed more often than other ones? Exploit there relative frequencies.
- Might access frequencies change over time? Use self-organizing structures like splay trees.
- Is the key close by? Use sequential search.
- Is my data structure sitting on external memory? Use B-trees.
- Can I guess where the key should be? Interpolation search
- Implementations : C++ STL
findandbinary_search - Related : Dictionaries, sorting
Median and Selection
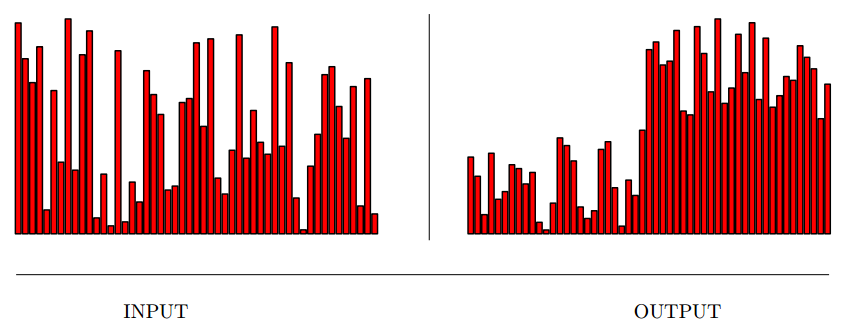
Input description: A set of \(n\) numbers or keys, and an integer \(k\).
Problem description: Find the key smaller than exactly \(k\) of the \(n\) keys.
- Median finding is an essential problem in statistics, more robust than mean.
- Special case of selection problem which arises in several applications,
- Filtering outlying elements : Remove 10% largest and smallest values.
- Identifying the most promising candidates : Select top 25%.
- Deciles and related divisions.
- Order statistics
- Issues in median finding(arbitrary selection),
- How fast does it have to be? \(O(n\log n)\) or \(O(n)\) expected-time.
- What if you only get to see each element once? Define approximate deciles, or do random sampling, or mix both strategies.
- How fast can you find the mode?
- Implementations : C++ STL
nth_element - Related : Priority queues, sorting
Generating Permutations
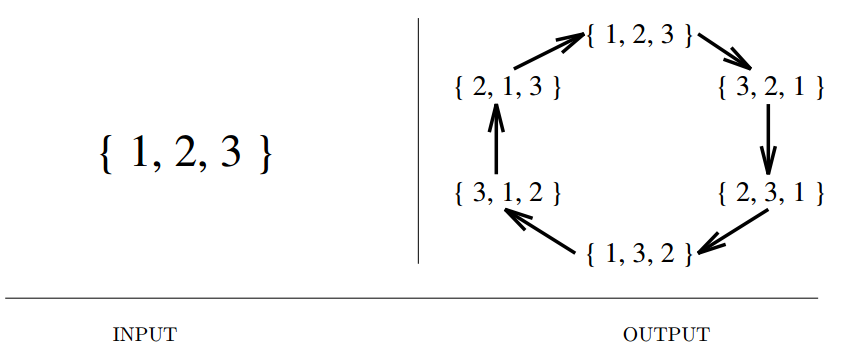
Input description: An integer \(n\).
Problem description: Generate (1) all, or (2) a random, or (3) the next permutation of length \(n\).
- Many algorithmic problems require seek the best way to order a set of objects, like travelling salesman, bandwidth, graph isomorphism.
- A fundamental notion of order is required.
- Two different paradigms : ranking/unranking and incremental change methods.
- Define functions Rank/Unrank such that, \(p = Unrank(Rank(p), n)\).
- Sequencing permutations
- Generating random permutations
- Keep track of a set of permutations.
- Incremental change algorithms can be tricky, but concise.
- We can also save time by avoiding identical permutations if there are duplicate elements.
- Implementations : C++ STL
next_permutationandprev_permutation. - Related : Random-number generation, generating subsets, generating partitions.
Generating Subsets
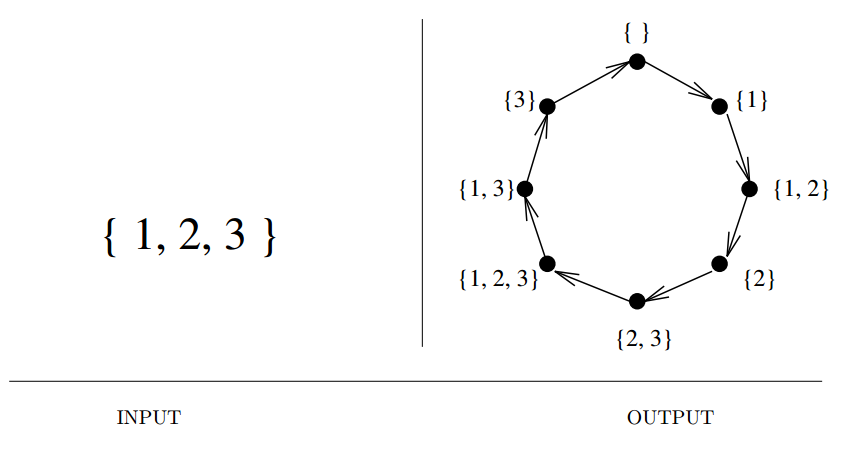
Input description: An integer \(n\).
Problem description: Generate (1) all, or (2) a random, or (3) the next subset of the integers \(\{1, \cdots , n\}\).
- Here, the order among the elements does not matter.
- Many algorithmic problems seek the best subset : vertex cover, knapsack, set packing.
- There are \(2^n\) different subsets of an \(n\)-element set. This is much less than the \(n!\) permutations.
- It is a good idea to keep elements in subset sorted in a canonical order so as to speed up identity testing.
- Options,
- Lexicographic order : surprisingly difficult to generate.
- Gray Code : Adjacent subsets differ by insertion/deletion of only one element.
- Binary counting : Use a bit-vector.
- Useful in,
- K-subsets All subsets of length K.
- Strings
- Related : Generating permutations, generating partitions
Generating Partitions
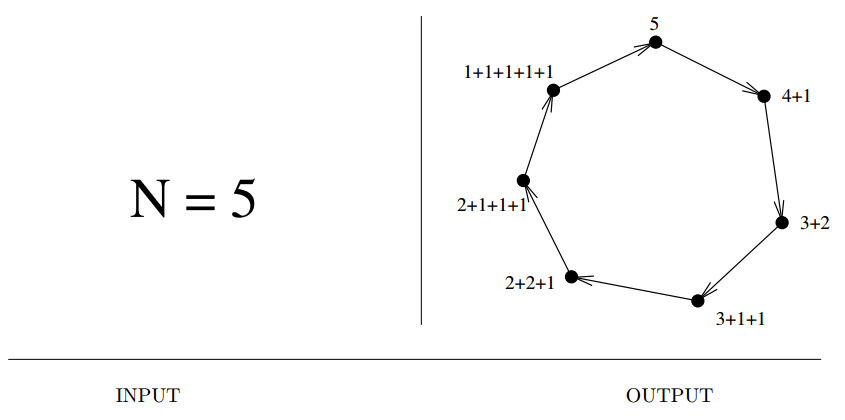
Input description: An integer \(n\).
Problem description: Generate (1) all, or (2) a random, or (3) the next integer or set partitions of length \(n\).
- Integer partitions are multisets of nonzero integers that add up exactly to \(n\). Use in for eg. nuclear fision..
- Set partitions divide the elements \(1, \ldots, n\) into nonempty subsets. Use in for eg. vertex/edge coloring and connected components.
- Related : Generating permutations, generating subsets.
Generating Graphs
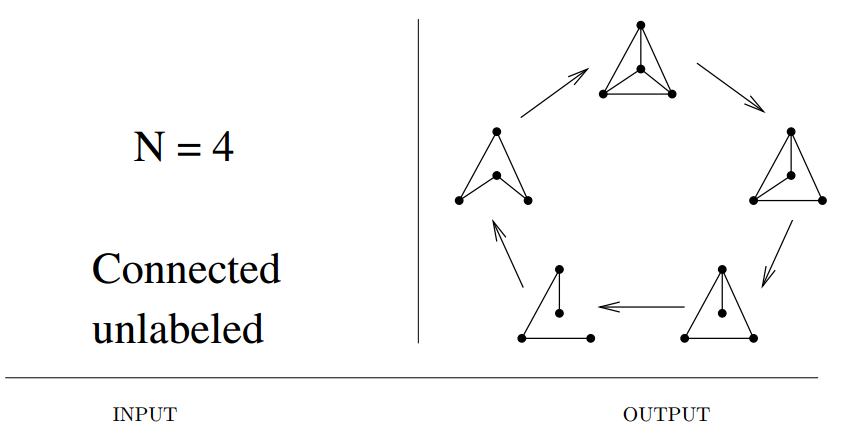
Input description: Parameters describing the desired graph, including the number of vertices \(n\), and the number of edges \(m\) or edge probability \(p\).
Problem description: Generate (1) all, or (2) a random, or (3) the next graph satisfying the parameters.
- Useful for generating test data for programs.
- A different application arises in network design. Adding redundancy and tolerance to vertex failures.
- Questions to ask,
- Do I want labeled or unlabeled graphs?
- Do I want directed or undirected graphs?
- How do you want to model randomness?
- Random edge generation
- Random edge selection
- Preferential attachment
- Alternatively, we can generate organic graphs that can reflect relationships among real-world objects.
- Other interesting graphs,
- Trees
- Fixed degree sequence graphs
- Implementations : Stanford GraphBase, Combinatorica, and more resources.
- Related : Generating permutations, graph isomorphism
Calendrical Calculations

Input description: A particular calendar date \(d\), specified by month, day, and year.
Problem description: Which day of the week did \(d\) fall on according to the given calendar system?
- Important in business applications. More important for international applications dealing with different timezones and possibly different calender systems.
- Complications arise with irregularity in years duration(leap years).
- So it becomes pointless to implement them by hand.
- Implementations : C++ Boost
datetime. - Related : Arbitrary precision arithmetic, generating permutations
Job Scheduling
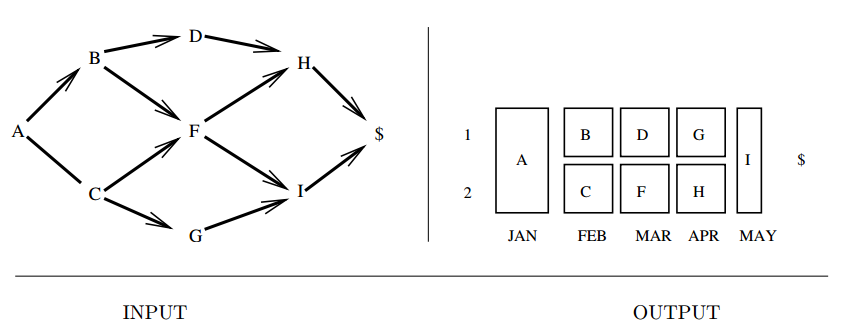
Input description: A directed acyclic graph \(G = (V,E)\), where vertices represent jobs and edge \((u,v)\) implies that task \(u\) must be completed before task \(v\).
Problem description: What schedule of tasks completes the job using the minimum amount of time or processors?
- Devising a proper schedule to satisfy a set of constraints is fundamental to many applications.
- Mapping tasks to processors is a critical aspect of any parallel-processing system.
- Applications
- Topological sorting : precedence constraints.
- Bipartite matching : skill matching
- Vertex and edge coloring : avoid interference.
- Travelling salesman
- Eulerian Cycle
- Interesting problems,
- Critical path
- Minimum completion time
- What is the tradeoff between the number of workers and completion time?
- Can also be modeled using Integer-linear programming.
- More variations,
- Assign jobs to identical machines to minimize the the total elapsed time.
- Tasks are provided with allowable start and required finish times.
- Implementations : JOBSHOP (C), Tablix, LEKIN and more.
- Related : Topological sorting, matching, vertex coloring, edge coloring, bin packing
Satisfiability
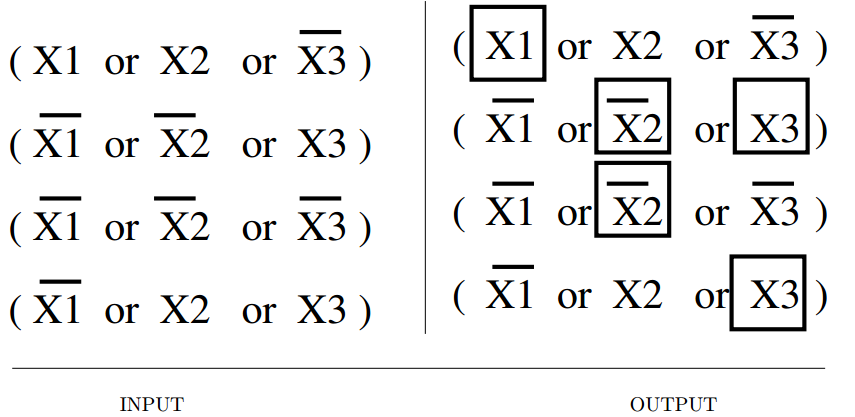
Input description: A set of clauses in conjunctive normal form.
Problem description: Is there a truth assignment to the Boolean variables such that every clause is simultaneously satisfied?
- A primary application of testing hardware/software design on all the inputs.
- The original NP-complete problem.
- Issues,
- Is your formula the
ANDofORs (CNF) or theORofANDs (DNF)? DNF can be solved easily, while CNF is NP-complete. We can use De Morgan's laws to convert CNF into DNF. However the translation itself could take exponential time. - How big are your clauses? 3-SAT and above are NP-complete.
- Does it suffice to satisfy most of the clauses? This can make the problem easier.
- Is your formula the
- Related : Constrained optimization, travelling salesman problem
Comments
comments powered by Disqus