Contents:
Computational Geometry
Robust Geometric Primitives
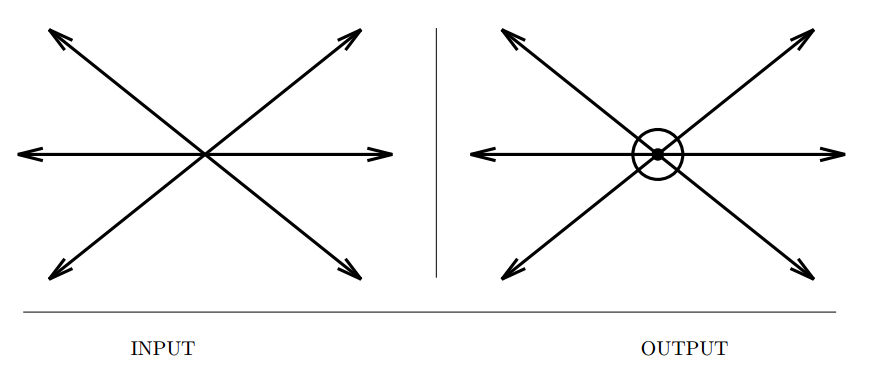
Input description: A point \(p\) and line segment \(l\), or two line segments \(l_1\), \(l_2\).
Problem description: Does \(p\) lie over, under, or on \(l\)? Does \(l_1\) intersect \(l_2\)?
- Even simple operations like line(segment) intersection can have many different cases including numerical stability and geometric degeneracy issues.
- Three primary approaches for dealing with degeneracy,
- Ignore it : Most common and recommended approach.
- Fake it : Random data perturbation so that it becomes non-degenerate.
- Deal with it : Write code to handle special degenerate cases
- Problems with overflows and numerical precision,
- Integer arithmetic : Force all the point coordinates to be fixed-size integers.
- Double precision reals : You may be able to avoid overflow and precision issues by using double precision for all the intermediate calculations and your data types.
- Arbitrary precision arithmetic : This is certain to be correct and slow.
- A set of low level geometric primitives :
- Area of a triangle
$$\begin{array}0 2.A(t) &=& \begin{vmatrix}a_x & a_y & 1\\ b_x & b_y & 1 \\ c_x & c_y & 1\end{vmatrix} \\&= &a_xb_y - a_yb_x + a_yc_x - a_xc_y + b_xc_y - c_xb_y\end{array}$$
This formula extends to \(d\)-dimensions, replacing \(2\) with \(d!\). - Above-below-on test : On which side of a line does a point lie?
- Line segment intersection : A line segment intersects a line iff its end points lie on different sides of the line.
- In-circle test : Check whether 4 given points lie on a circle,
$$\begin{array}0 incircle(a,b,c,d) &=& \begin{vmatrix}a_x & a_y & a_x^2+a_y^2&1\\ b_x & b_y & b_x^2+b_y^2 & 1 \\ c_x & c_y & c_x^2+c_y^2 & 1\\d_x & d_y & d_x^2+d_y^2 & 1\end{vmatrix} \\\end{array}$$This will return 0 if all four points are cocircular, a positive value if \(d\) is inside the circle, and negative if \(d\) is outside.
- Area of a triangle
- Implementations : CGAL, LEDA.
- Related : Intersection detection, maintaining arrangement.
Convex Hull
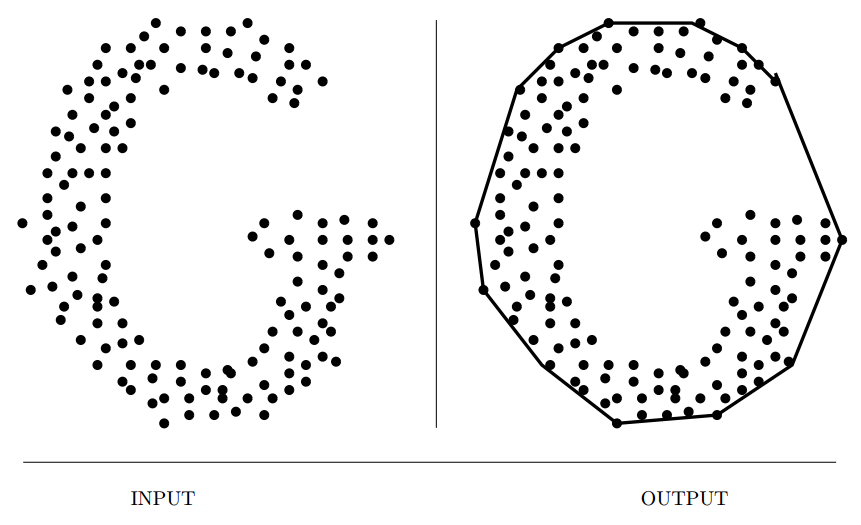
Input description: A set \(S\) of \(n\) points in \(d\)-dimensional space.
Problem description: Find the smallest convex polygon (or polyhedron) containing all the points of \(S\).
- The most important problem in elementary computational geometry, just as sorting is the most important elementary problem in combinatorial algorithms.
- Serves as a first preprocessing step to many geometric algorithms.
- As many convex hull algorithms as sorting algorithms. How to choose,
- How many dimensions are you working with? Certain assumptions break down in higher dimensions. For higher dimensions use a library method.
- Is your data given as vertices or half-spaces? These are dual of each other.
- How many points are likely to be on the hull? Topmost, leftmost, bottom-most and rightmost points would certainly be on the hull, and points lying in the region enclosed by these vertices can be discarded in one sweep. This can also be used in higher dimensions.
- How do I find the shape of my point set? Convex hulls would loose most of the shape information details.
- Graham scan is the primary algorithm.
- Start with a point \(p\) known to be on the hull.
- Sort all the points by their angular coordinates around \(p\).
- Starting with the smallest, move counter-clockwise, adding points to the hull.
- Remove last point if they form a concavity, i.e. an angle greater than \(180°\).
- Total time, \(O(n \lg n)\)
- Implementations : CGAL, LEDA, Qhull
- Related : Sorting, Vornoi diagrams
Triangulation

Input description: A set of points or a polyhedron.
Problem description: Partition the interior of the point set or polyhedron into
triangles.
- Useful in finite element analysis to computer graphics.
- Some specific issues arising in triangulation,
- Are you triangulating a point set or a polygon? First find the convex hull of points.
- Does the shape of the triangles in your triangulation matter?
- How can I improve the shape of a given triangulation? By edge-flipping internal triangles.
- What dimension are we working in? NP-complete if we dont cant add extra vertices.
- What constraints does the input have?
- Are you allowed to add extra points or move input vertces?
- Implementations : CGAL, LEDA, and more.
- Related : Vornoi diagrams, polygon partitioning
Vornoi Diagrams
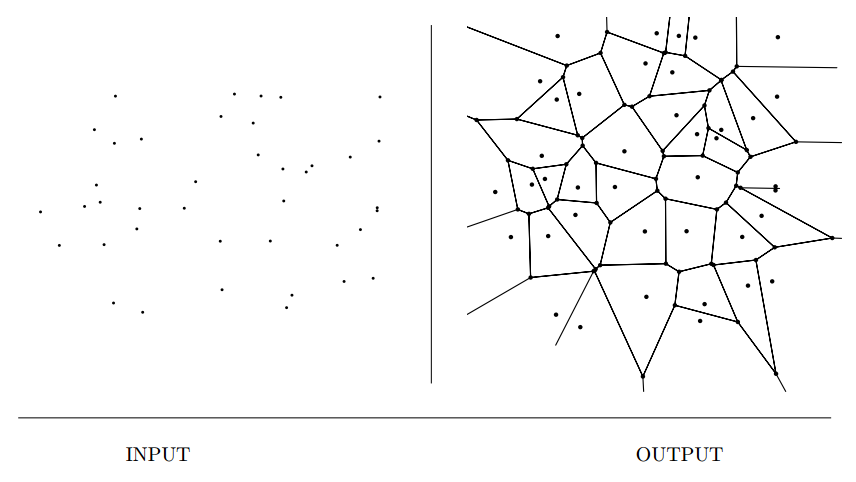
Input description: A set \(S\) of points \(p_1, \ldots , p_n\).
Problem description: Decompose space into regions around each point such that
all points in the region around \(p_i\) are closer to \(p_i\) than any other point in \(S\).
- Vornoi diagrams represent the region of influence around each of a given set of sites.
- They have a surprising variety of applications,
- Nearest Neighbour search : Select the cell.
- Facility location : Choose a vertex.
- Largest empty circle : Choose a vertex.
- Path planning : Stick to the edges.
- Quality triangulations : Delauny triangulations can be easily constructed as dual of the Voirnoi diagram.
- Each edge is a perpendicular bisector between two points in \(S\).
- Fortune's sweepline algorithm runs in optimal \(O(n\log n)\).
- Interesting relationship between convex hulls(in \(d+1\) dimensions) and vornoi diagrams(in \(d\) dimensions) : Project each point \(E^d(x_1,x_2, \ldots , x_d)\) to point \((x_1, x_2, \ldots, x_d, \sum_{i=1}^{d}x_i^2)\), take the convex hull in \(d+1\) dimensions and project back to \(d\) dimensions.
- This is the best way to construct Vornoi diagrams in higher dimensions.
- Variations of standard Vornoi diagrams that arise in practice,
- Non-Euclidean distance metric
- Power diagrams : Non uniform power of influence over space.
- K-th order and furthest-site diagrams :
- Implementations : CGAL, LEDA, Qhull, and more.
- Related : Nearest neighbor search, point location, triangulation
Nearest Neighbor Search
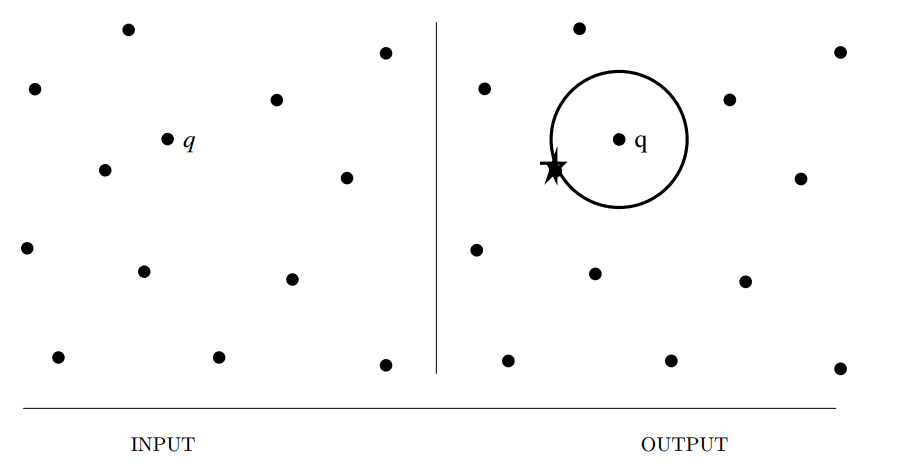
Input description: A set \(S\) of \(n\) points in \(d\) dimensions; a query point \(q\).
Problem description: Which point in \(S\) is closest to \(q\)?
- Arises in numerous applications across the board.
- Is also important in classification and image compression(vector-quantization).
- Issues arising in nearest-neighbor search include:
- How many points are you searching? Only when the number of points is high, it pays to consider sophisticated approaches.
- How many dimensions are you working in? Gets progressively harder as the dimensionality increases. \(kd-\) tree data structure can be very useful here, but only upto a certain number of dimensions(20). Vornoi diagrams also prove to be an efficient data structure, but often become unusable at higher dimensions.
- Do you really need the exact nearest neighbor? Heuristics can give a reasonable answer fairly quickly. Dimensionality reduction also becomes very handy.
- Is your data set static or dynamic? Static structures can be more efficient.
- Implementations : ANN, KDTREE 2, CGAL, LEDA, and more,...
- Related :Kd-trees, Vornoi diagrams, range search
Range Search
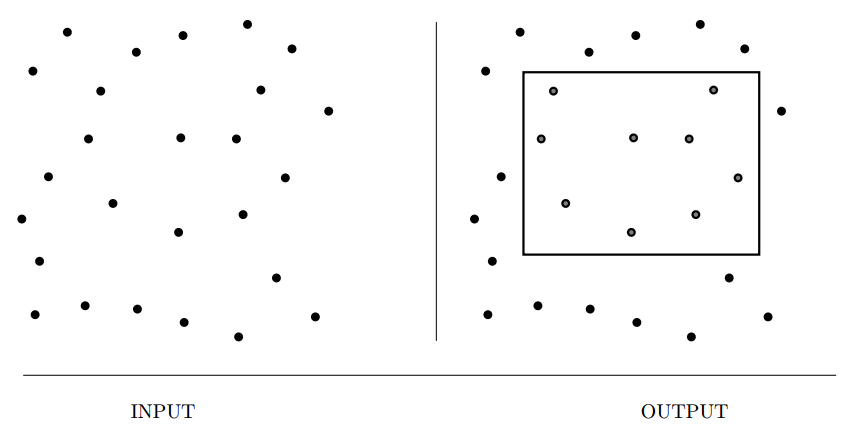
Input description: A set \(S\) of \(n\) points in \(E_d\) and a query region \(Q\).
Problem description: What points in \(S\) lie within \(Q\)?
- Arises often in database and GIS applications.
- The difficulty of range search depends on the following factors,
- How many range queries are you going to perform? - Brute force works just fine when the number ois small.
- What shape is your query polygon? - Axis-parallel rectangles are easiest to query against. Use decomposition for non-convex polygons.
- How many dimensions?
- Is your point set static?
- Can I just count the number of points in a region, or do I have to identify them?
- Implementations : CGAL, LEDA, ANN, Ranger
- Related : Kd-trees, point location
Point Location
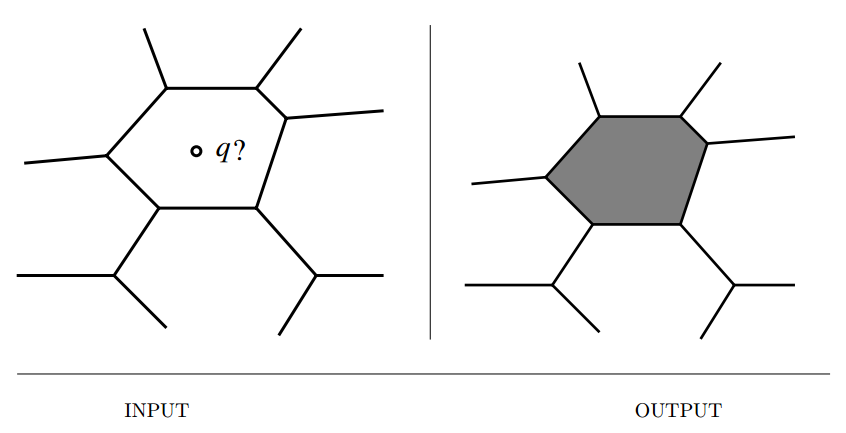
Input description: A decomposition of the plane into polygonal regions and a query point \(q\).
Problem description: Which region contains the query point \(q\)?
- Variations to the simple problem,
- Is a given point inside or outside of polygon P? Count how many times a ray originating from the query point intersects the polygon.
- How many queries must be performed? It could be more beneficial to construct a grid like structure.
- How complicated are the regions of your subdivision? Either perform a triangulation first, or compute a grid-like structure.
- How regularly sized and spaced are your regions? Use (irregular) grid like structures.
- How many dimensions will you be working in? For higher dimensions, \(Kd\)-trees might be a better choice.
- Am I close to the right cell?
- Implementations : CGAL, LEDA, ANN, Arrange
- Related : Kd-trees, Vornoi diagrams, nearest neighbor search
Intersection Detection
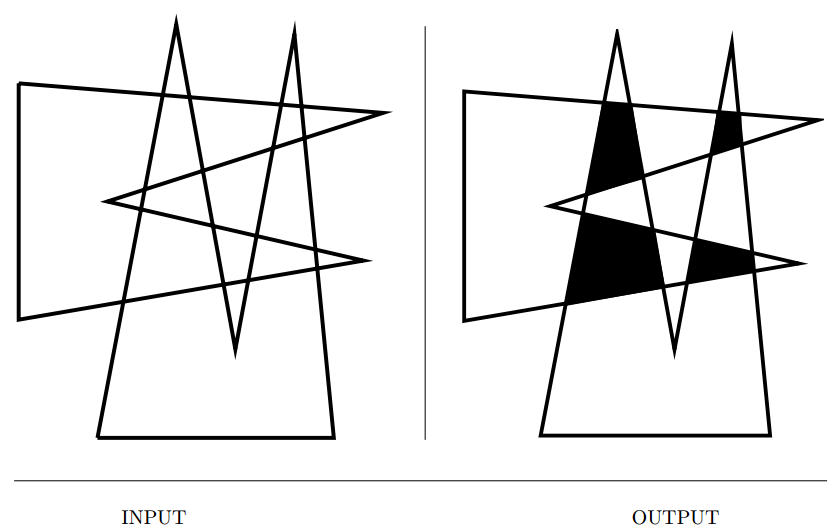
Input description: A set \(S\) of lines and line segments \(l_1, \ldots , l_n\) or a pair of polygons or polyhedra \(P_1\) and \(P_2\).
Problem description: Which pairs of line segments intersect each other? What is the intersection of \(P_1\) and \(P_2\)?
- Numerous applications from collision detection to error checking in VLSI design.
- Issues arising in intersection detection include,
- *Do you want to compute the intersection or just report it? Detection can be substantially easier.
- Are you intersecting lines or line segments? Lines(or rays) can be easier than line segments.
- How many intersection points do you expect?
- Can you see point x from point y? Visibility/Occlusion queries.
- Are the intersecting objects convex?
- Are you searching for intersections repeatedly for the same basic objects? Using simpler bounding boxes can help improve the overall performance.
- Planar sweep algorithms can be used to efficiently compute the intersections for a set of line segments.
- Implementations LEDA, CGAL, and more.
- Related : Maintaining arrangements, motion planning
Bin Packing
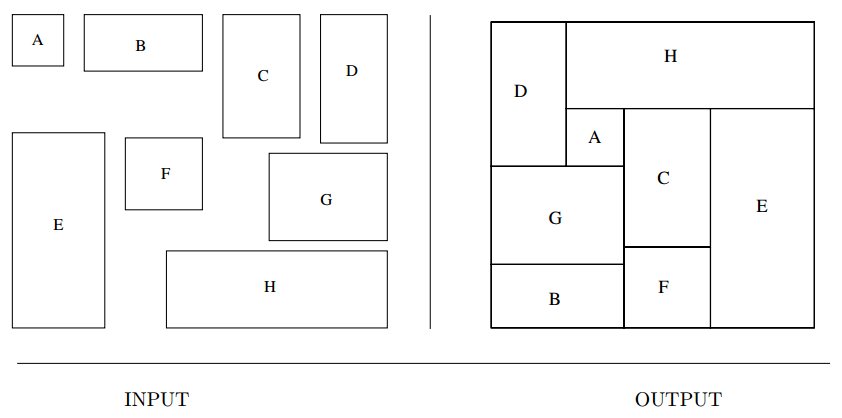
Input description: A set of \(n\) items with sizes \(d_1, \ldots , d_n\). A set of \(m\) bins with capacity \(c_1, \ldots , c_m\).
Problem description: Store all the items using the smallest number of bins.
- Arises in a variety of packaging and manufacturing problems.
- Eg. manufacturing widgets cut from sheet metal pr pants cut from cloth. To minimize cost and waste, is a bin-packing variant called cutting-stockproblem.
- Even the most elementary sounding problems of bin-packing are NP-complete(Integer partition).
- Factors affecting the choice of heuristic,
- What are the shapes and sizes of the objects? One dimensional bin-packing(or two dimensional boxes with same width) becomes a special case of knapsack problem.
- Are there constraints on the orientation and placement of objects? Different boxes may have different constraints. Many people just ignore the constraints, but you may not be able to.
- Is the problem on-line or off-line? We can do a better job if we know all the constraints beforehand, and we can plan ahead.
- Biggest objects first, turns out to be the best heuristics.
- For non-rectangular shapes, bounding boxes can be used.
- More sophisticated algorithms are available.
- Related : Knapsack problem, set packing,
Medial-Axis Transform

Input description: A polygon or polyhedron \(P\).
Problem description: What are the set of points within \(P\) that have more than one closest point on the boundary of \(P\)?
- Useful in thinning a polygon, or as is sometimes said, finding its skeleton.
- The skeleton is useful in many contexts, like shape reconstruction and motion planning.
- Always a tree for polygons(without holes). DP can be used to find the edit-distance between two skeletons.
- Two distinct images,
- Geometric data : Vornoi diagram of line segments can be used. The portion of the vornoi diagram that lies in the polygon is the skeleton.
- Image data : Geometric approach can be used by converting the image data into geometric regions.
Pixel-based approaches can also be used, but they tend not to be very accurate, because of the differences in the continuos and discrete world.
- Implementations : CGAL, VRNOI,
- Related : Vornoi diagrams, minkowski sum
Polygon Partitioning
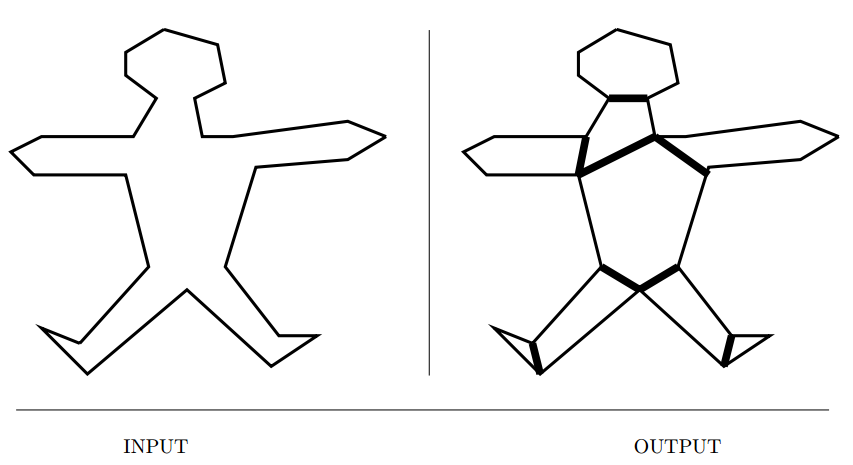
Input description: A polygon or polyhedron \(P\).
Problem description: Partition \(P\) into a small number of simple (typically convex) pieces.
- Important preprocessing step for many geometric algorithms.
- Several flavors of polygon partitioning,
- Should all the pieces be triangles? This would not produce the smallest number of partitions.
- Do I want to cover or partition my polygon? Partitioning only allows mutually non-overlapping pieces.
- Am I allowed to add extra vertices? Adding (steiner) vertices may result in smaller number of partitions(but with a more complicated algorithm).
- Hertel-Mehlhorn heuristic, start with an arbitrary triangulation, and delete chords until it leaves only convex pieces.
- DP finds the absolute minimum partitions in \(O(n^4)\).
- Related : Triangulation, set cover
Simplifying Polygons

Input description: A polygon or polyhedron \(p\), with \(n\) vertices.
Problem description: Find a polygon or polyhedron \(p'\) containing only \(n'\) vertices, such that the shape of \(p'\) is as close as possible to \(p\).
- Two primary applications,
- Cleaning up a noisy representation of a shape,
- Data compression, reduce detail on large objects(LOD)
- Several issues arise,
- Do you want the convex hull? Can be useful in some applications(mmotion planning), and can be disastrous in some(OCR system).
- Am I allowed to insert or just delete points? Local modifications to reduce the vertex count are done. Most robust heuristics move the vertices around to cover up the gaps created by deletions. Must the resulting polygon be intersection-free? Simplicity(non-self intersection) can be difficult to achieve for some shapes.
- Are you given an image to clean up instead of a polygon to simplify? Conventionally, Fourier transform is used to clean up images.
- Related : Fourier transform, convex hull
Shape Similarity
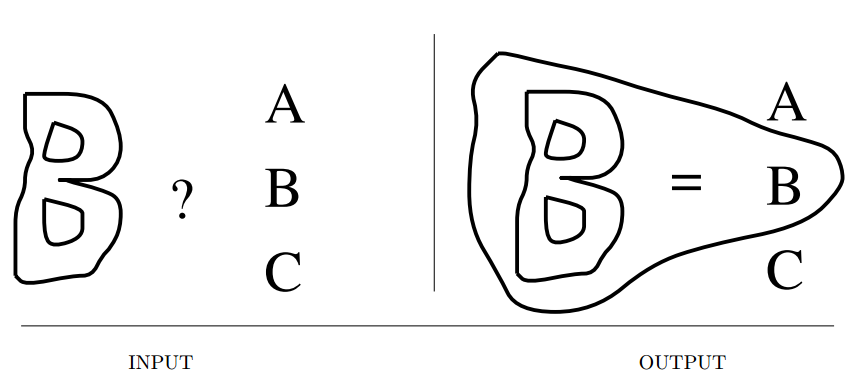
Input description: Two polygonal shapes, \(P_1\) and \(P_2\).
Problem description: How similar are \(P_1\) and \(P_2\)?
- We seek to identify the unknown shapes by matching them to the most similar shape models.
- What similar means can be application dependent.
- Possible approaches are,
- Hammming distance, measures the area of symmetric difference between the two polygons. Zero for identical and aligned polygons. Problem is simply finding the union and intersection of polygons, further simplified if rotation is constrained.
However, this only captures a crude notion of shape, and might be ineffective in most applications. - Hausdorff distance, identifies the maximum distance for two points on \(P_1\) and \(P_2\).
- Comparing skeletons, this problem then reduces to subgraph isomorphism.
- Support Vector Machines, or other learning based approaches such as neural networks.
- Hammming distance, measures the area of symmetric difference between the two polygons. Zero for identical and aligned polygons. Problem is simply finding the union and intersection of polygons, further simplified if rotation is constrained.
- Related : Graph isomorphism, thinning
Motion Planning
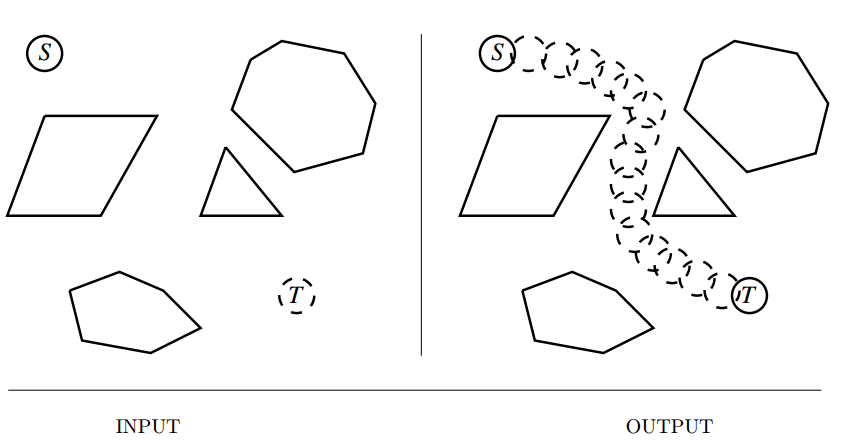
Input description: A polygonal-shaped robot starting in a given position \(s\) in a room containing polygonal obstacles, and a goal position \(t\).
Problem description: Find the shortest route taking \(s\) to \(t\) without intersecting any obstacles.
- Robots, computer animation, molecular docking, and more,..
- Many factors govern the complexity of motion planning problems,
- Is your robot a point? Build the visibility graph using the polygons and the source and target vertices. Perform Dijkstra's shortest path from \(s\) to \(t\).
- What motions can your robot perform? Size of the bot, degrees of freedom.
- Can you simplify the shape of your robot? Anything you can simplify will be a big win. Try replacing it with an enclosing disc.
- Are motions limited to translation only?
- Are the obstacles known in advance?
- Implementations : The Motion Planning Toolkit*, CGAL
- Related : Shortest path, Minkowski sum
Maintaining Line Alignments
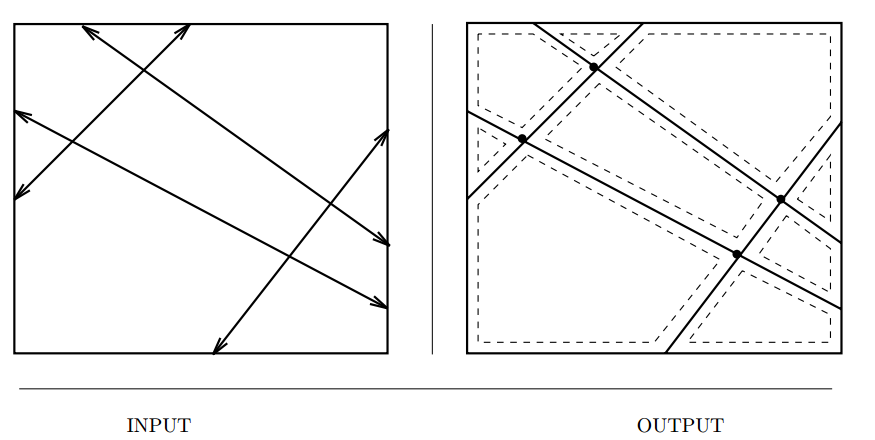
Input description: A set of lines and line segments \(l_1, \ldots , l_n\).
Problem description: What is the decomposition of the plane defined by \(l_1, \ldots , l_n\)?
- Examples,
- Degeneracy testing
- Satisfying the maximum number of linear constraints
- Issues arising in arrangements include,
- What is the right way to construct a line arrangement? Incremental?
- How big will your arrangements be?
- What do you want to do with your arrangement?
- Does your input consist of points instead of lines? Points represent the dual problem,
$$L : y = 2ax - b \leftrightarrow p : (a,b)$$
This is surprisingly the same problem in many cases.
- Related : Intersection detection, point location
Minkowski Sum
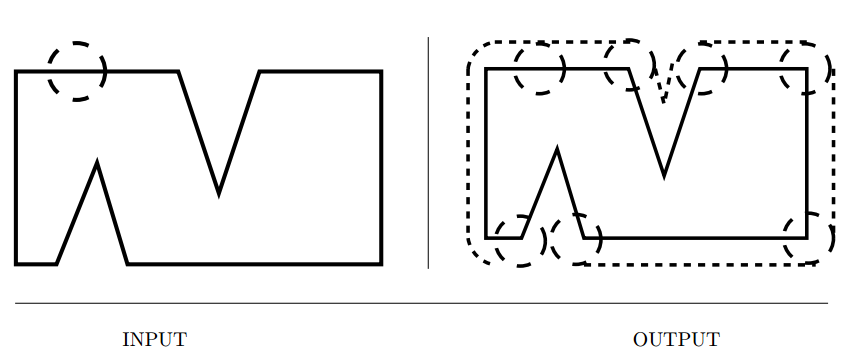
Input description: Point sets or polygons \(A\) and \(B\), containing \(n\) and \(m\) vertices respectively.
Problem description: What is the convolution of \(A\) and \(B\) — i.e. , the Minkowski
sum \(A + B = {x + y|x \in A, y \in B}\)?
- Very interesting geometric operations that can fatten objects in appropriate ways.
- Eg. For robot motion planning, transform the space by taking Minkowski sum of the obstacles and the shape of the robot, reducing the problem to point robots.
- Also helpful in shape simplification and smoothing.
- Issues arising in Minkowski sum,
- Are your objects rasterized images or explicit polygons? Polygonal representations can get more complicated.
- Do you want to fatten your object by a fixed amount? Just use a circular disk with offset as radius.
- Are your objects convex or non-convex? This can become ugly and majestic with surprising results for non-convex polygons.
- Related : Thinning, motion planning, simplifying polygons
Comments
comments powered by Disqus