Contents:
Graph Problems : Polynomial-Time
Connected Components
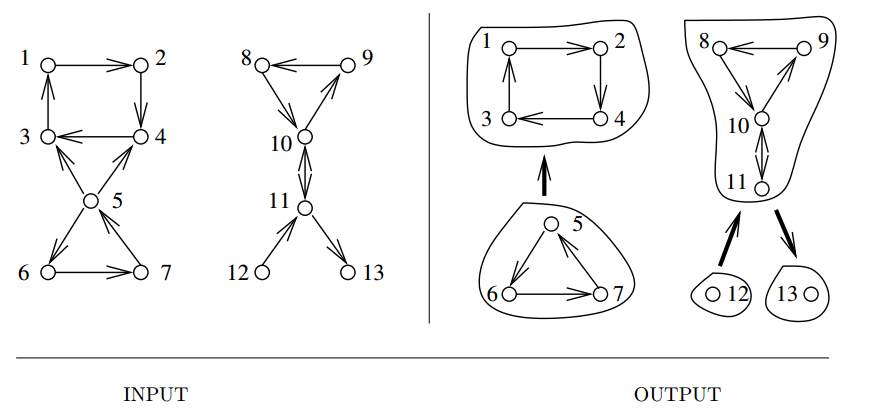
Input description: A directed or undirected graph \(G\).
Problem description: Identify the different pieces or components of \(G\), where vertices
\(x\) and \(y\) are members of different components if no path exists from \(x\) to \(y\) in \(G\).
- Associated problems
- Identify natural clusters in a set of items.
- Also used as a preprocessing step to test whether a graph is connected.
- Other notions of connectivity,
- What if my graph is connected? Weekly or strongly connected?
Weekly connected components can be identified by a single DFS or BFS traversal. For strongly connected components, check whether the graph is weekly connected, then check again on the reversed graph. - What is the weakest point in my graph/network?
- Is the graph a tree? How can I find a cycle if cone exists?
- Implementations
- C++ : Boost Graph Library, LEDA
- Java : JUNG, JGraphT
- Related : Edge-vertex connectivity, shortest path
Topological Sort
Input description: A directed acyclic graph \(G = (V,E)\), also known as a partial order
or poset.
Problem description: Find a linear ordering of the vertices of \(V\) such that for
each edge \((i,j) \in E\), vertex \(i\) is to the left of vertex \(j\).
- Arises as a subproblem in most algorithms on DAGs.
- Plays the same role for DAGs as depth-first search plays for general graphs.
- Can be used to schedule tasks under precedence constraints.
- Only DAGs can be topologically sorted, any directed cycle would provide an inherent contradiction to linear order of tasks.
- Every DAG can be topologically sorted.
- DAGs can be often topologically sorted in many different ways.
- Simple linear time algorithm :
- Find source vertices(zero in-degree) using DFS.
- Eliminate source vertices and edges, find new source vertices and place then next in the schedule.
- Repeat.
- Special considerations,
- What if I need all the linear extensions, instead of just one of them?
NP-hard, use backtracking. - What if your graph is not acyclic?
Remove the smallest set of edges(feedback arc set) or vertices(feedback vertex set) so as to create a DAG. Also NP-hard.
- What if I need all the linear extensions, instead of just one of them?
- Implementations :
- C++ : Boost Graph Library, LEDA
- Java : JDSL, JGraphT
- Related : Sorting, feedback edge/vertex set
Minimum Spanning Tree

Input description: A graph \(G = (V,E)\) with weighted edges.
Problem description: The minimum weight subset of edges \(E' \subset E\) that form a
tree on \(V\).
- MST defines the cheapest subset of edges that keep the graph in one connected component.
- Can be compute quickly and easily, and create a sparse subgraph that reflects a lot about the original graph.
- They provide a way to identify clusters in sets of points.
- They can be used to give approximate solutions to hard problems such as Steiner tree and traveling salesman.
- As an educational tool, MST algorithms provide graphic evidence that greedy algorithms can give provably optimal solutions.
- Kruskal's algorithm.
- Each vertex starts as a separate tree and these trees merges together by repeatedly adding the lowest cost edge that spans two distinct subtrees (i.e. , does not create a cycle).
- Efficiently implemented using union-find data structure.
- Prim's algorithm.
- Starts with an arbitrary vertex and grows a tree from it, repeatedly finding the lowest-cost edge that links some new vertex into this tree.
- Implemented using priority queues.
- Boruvka's algorithm
- Rests on the observation that the lowest-weight edge incident on each vertex must be in the minimum spanning tree. The union of these edges will result in a spanning forest of at most \(n/2\) trees. Now for each of these trees \(T\), select the edge \((x,y)\) of lowest weight such that \(x \in T\) and $y \notin T $.
- Repeat till a single tree is created.
- Questions to ask,
- Are the weights of all the edges of your graph identical? MST can be found using DFS or BFS.
- Should I use Prim’s or Kruskal’s algorithm?
Prim’s algorithm is faster on dense graphs, while Kruskal’s is faster on sparse graphs - What if my input is points in the plane, instead of a graph?
First run Delaunay triangulation, then find MST on that graph. - How do I find a spanning tree that avoids vertices of high degree?
NP-Complete, identical to Hamiltonian path problem. However efficient approximation algorithms exist.
- Implementations : Boost, LEDA, and more.
- Related : Steiner tree, travelling salesman
Shortest Path
Input description: An edge-weighted graph \(G\), with vertices \(s\) and \(t\).
Problem description: Find the shortest path from \(s\) to \(t\) in \(G\).
- Applications,
- Most obvious applications arise in transportation or communications.
- Image segmentation. requires modelling the graph with proper transitions.
- Differentiate homophones, words that sound similar.
- For informative visualization of graphs. Keep the center at the center.
- Dijkstra's algorithm : single source shortest path on positively weighted graphs.
- Questions to ask,
- Is your graph weighted or unweighted?
If unweighted, a simple BFS would do. If weighted use Dijkstra's algorithm. - Does your graph have negative cost weights?
Use Bellman-Ford algorithm. If negative cost cycles are present, then the problem is ill defined. - Is your input a set of geometric obstacles instead of a graph?
Dijkstra's algorithm would work, but there are faster algorithms for this setting. - Is your graph acyclic? i.e. a DAG?
Use topological sort. - Do you need the shortest path between all pairs of points?
Use Floyd-Warshall algorithm - How do I find the shortest cycle in a graph?
Floyd's algorithm can do that. Finding longest cycle is similar to Hamiltonian cycle, and is NP-complete.
- Is your graph weighted or unweighted?
- Other graph properties are related,
- Eccentricity of a vertex is the shortest-path distance to the farthest vertex.
- Radius of a graph is the smallest eccentricity.
- Center is the set of vertices whose eccentricity is the radius.
- Diameter of a graph is the maximum eccentricity of any vertex.
- Implementations :
- C++ : MLB, Boost, LEDA and more.
- Related : Network flow, motion planning
Transitive Closure and Reduction
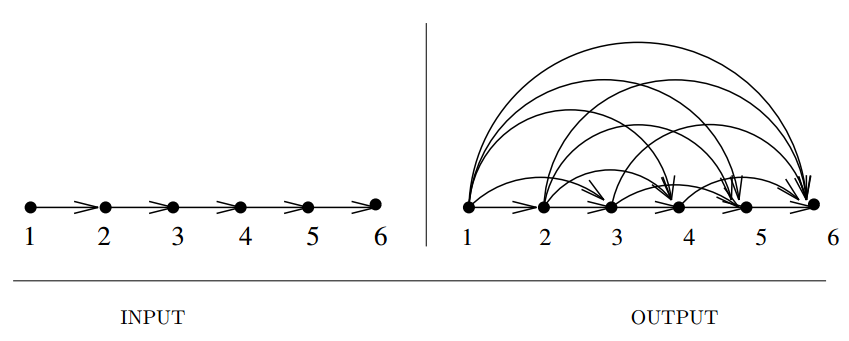
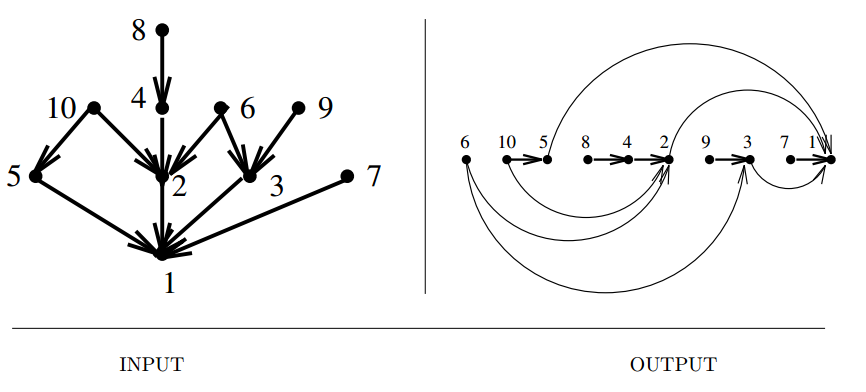
Input description: A directed graph \(G = (V,E)\).
Problem description: For transitive closure, construct a graph \(G' = (V, E')\) with
edge \((i, j) \in E'\) iff there is a directed path from \(i\) to \(j\) in \(G\). For
transitive reduction, construct a small graph \(G' = (V, E')\) with a directed path from \(i\)
to \(j\) in \(G'\) iff there is a directed path from \(i\) to \(j\) in \(G\).
- Transitive closure can be thought of as establishing a data structure that makes it possible to solve reachability questions efficiently.
- The simplest algorithm just performs a breadth-first or depth-first search from each vertex and keeps track of all vertices encountered. But this degenerates to cubic time on dense graphs.
- Can also use Warshall's algorithm, or use matrix multiplication.
- The problem can be greatly reduced if we only consider the strongly connected components.
- Transitive reduction (also known as minimum equivalent digraph) is the inverse operation of transitive closure, reducing the number of edges, while maintaining identical reachability properties.
- Primary application in space minimization, reducing redundancy, remove clutter while visualization.
- However, there are multiple identifying formulations of the problem
- A linear-time, quick-and-dirty transitive reduction algorithm identifies the strongly connected components of G, replaces each by a simple directed cycle, and adds these edges to those bridging the different components.
- Implementations : Boost Graph, LEDA, Graphlib(Transitivity) and more.
- Related : Connected components, shortest path
Matching
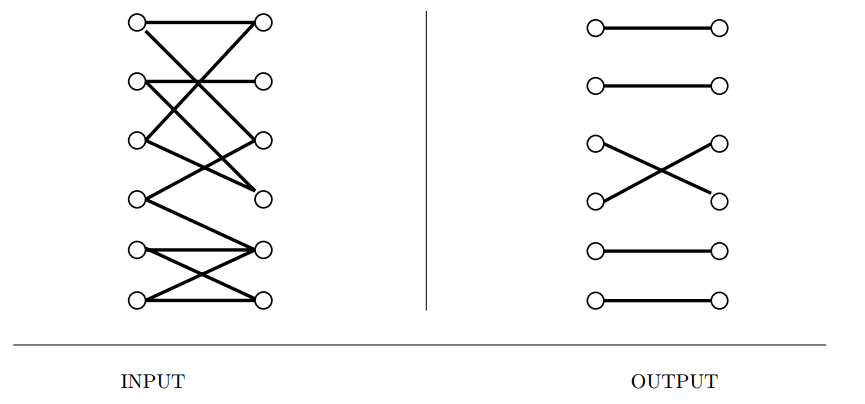
Input description: A (weighted) graph \(G = (V,E)\).
Problem description: Find the largest set of edges \(E'\) from \(E\) such that each
vertex in \(V\) is incident to at most one edge of \(E'\).
- The basic matching problem can be formulated in many different forms while remaining essentially the same assignment problem.
- Is your graph bipartite? Then things will be simpler.
- What if certain employees can be given multiple jobs? This can be modeled by replicating the employee(or job) as many times as needed.
- Is your graph weighted or unweighted? Most problems would be unweighted, but the same can be modeled on weighted graphs, where we require to construct maximum weight matching.
- Standard algorithms for bipartite matching are based on network flow.
- Implementations : CSA, BIM, GOBLIN, LEDA, Blossum IV, Stanford GraphBase and more.
- Related : Eulerian Cycle, network flow
Eulerian Cycle/Chinese Postman
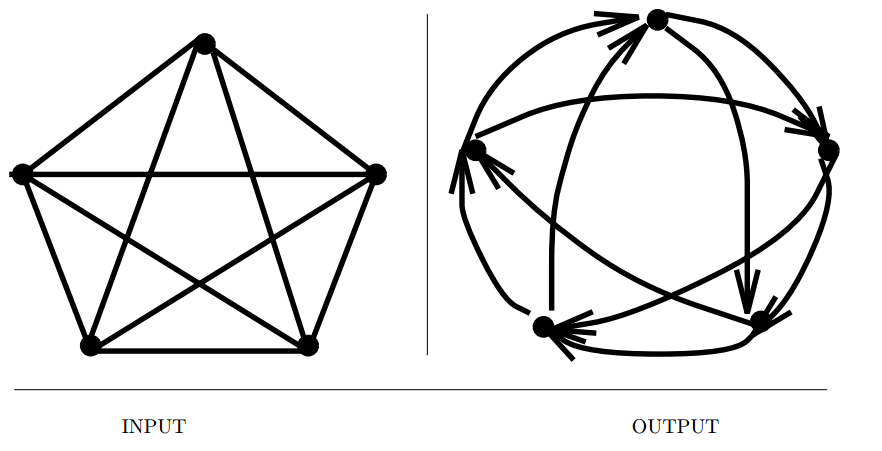
Input description: A graph \(G = (V,E)\).
Problem description: Find the shortest tour visiting each edge of \(G\) at least once.
- This problem is has many applications and variants.
- These are a few conditions that can determine if a Eulerian cycle or path exists,
- An undirected graph contains an Eulerian cycle iff (1) it is connected, and (2) each vertex is of even degree.
- An undirected graph contains an Eulerian path iff (1) it is connected, and (2) all but two vertices are of even degree. These two vertices will be the start and end points of any path.
- A directed graph contains an Eulerian cycle iff (1) it is strongly-connected, and (2) each vertex has the same in-degree as out-degree.
- Finally, a directed graph contains an Eulerian path from x to y iff (1) it is connected, and (2) all other vertices have the same in-degree as out-degree, with x and y being vertices with in-degree one less and one more than their out-degrees, respectively.
- This characterization of Eulerian graphs makes it easy to test and explicitly create a cycle.
- The chinese postman problem minimizes the length of a cycle that traverses every edge at least once.
- Related : Matching, Hamiltonian Cycle
Edge and Vertex Connectivity
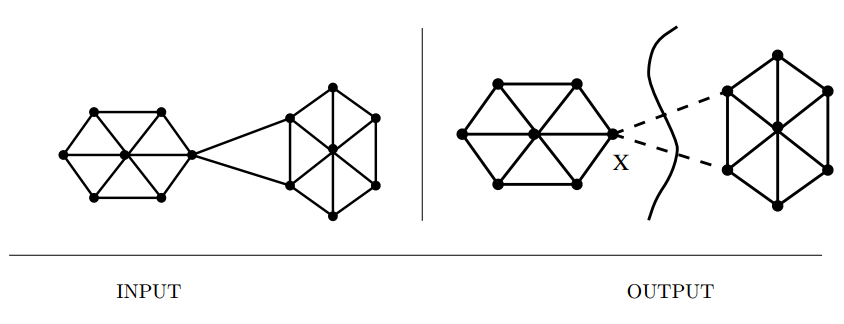
Input description: A graph \(G\). Optionally, a pair of vertices \(s\) and \(t\).
Problem description: What is the smallest subset of vertices (or edges) whose
deletion will disconnect \(G\)? Or which will separate \(s\) from \(t\)?
- The edge (vertex) connectivity of a graph \(G\) is the smallest number of edge (vertex) deletions sufficient to disconnect \(G\).
- Is the graph already disconnected?
- Is there one weak link in my graph?
- What if I want to split the graph into equal sized pieces?
- Are arbitrary cuts OK, or must I separate a given pair of vertices?
- Edge and vertex connectivity can both be found using network-flow techniques.
- Related : Connected components, network flow
Network Flow
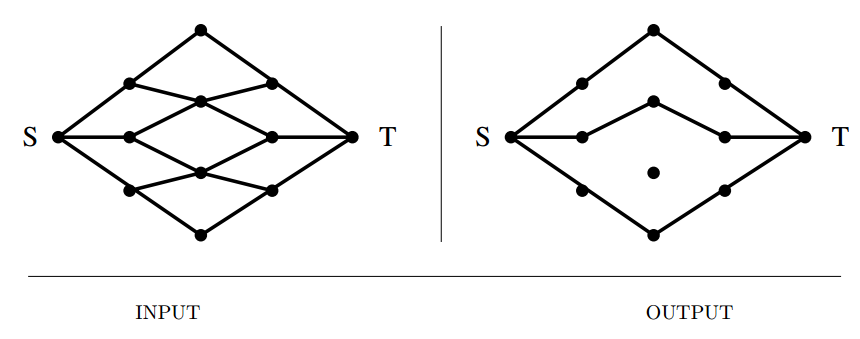
Input description: A directed graph \(G\), where each edge \(e = (i,j)\) has a capacity
\(c_e\). A source node \(s\) and sink node \(t\).
Problem description: What is the maximum flow you can route from \(s\) to \(t\) while
respecting the capacity constraint of each edge?
- Goes far beyond plumbing.
- A surprising variety of linear programming problems can be modeled as network-flow problems.
- And, network flow algorithms can solve these problems much faster than general purpose linear programming methods.
- Two primary classes of problems,
- Maximum Flow
- Minimum Cost flow
- Special considerations,
- What if I have multiple sources/sinks? Add a vertex to create super source/sink.
- What if all arc capacities are identical, either 0 or 1? Faster algorithms exist.
- What if all my edge costs are identical?
- What if I have multiple types of material moving through the network? multicommodity flow
- Primary classes of algorithms,
- Augmenting path methods
- Preflow-push methods
- Related : Linear programming, matching, connectivity
Drawing Graphs Nicely
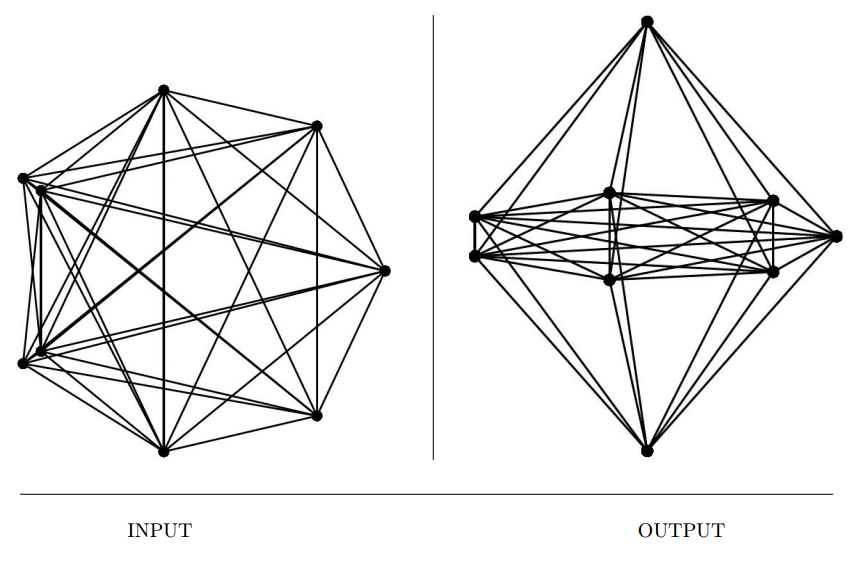
Input description: A graph \(G\).
Problem description: Draw a graph \(G\) so as to accurately reflect its structure.
- What exactly does a nice drawing mean?
- Several criteria can be used,
- Crossings,
- Area,
- Edge length,
- Angular resolution,
- Aspect ratio
- Unfortunately, these goals are mutually contradictory and the problem is NP-complete.
- Also, drawing the complete graph, with more than 15 to 20 vertices, would not look particularly nice in the absence of any inherent symmetry.
- Some questions to ask,
- Must the edges be straight, or can I have curves/bends?
- Is there a natural, application specific drawing? use it if it exists.
- Is your graph either planer or a tree?
- Is your graph directed?
- How fast must your algorithm be? Use incremental updates for interactive applications.
- Does your graph contain symmetries?
- First quick and dirty method, place all the vertices in a circle, and start adding the edges.
- Simulated annealing can be used to minimize the crossings.
- A general purpose heuristic can model the graph as a system of springs and then use enerygy minimization to space the vertices.
- After the graph is drawn, you may also want to place the edge/vertex labels. This, can be shown to be NP-complete, but heuristics can be used effectively.
- Also related problem of graph visualization in 3 dimensions.
- Implementations : GraphViz.
- Related : Drawing trees, planarity testing
Drawing Trees
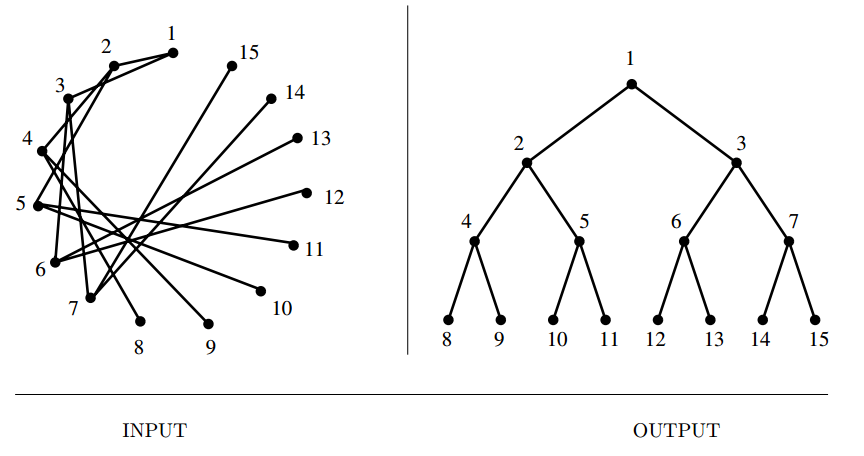
Input description: A tree \(T\), which is a graph without any cycles.
Problem description: Create a nice drawing of the tree \(T\).
- Are you drawing a free or a rooted tree.
- Rooted trees define a hierarchical order.
- Free trees do not encode any structure beyond their connection topology(e.g. a Minimum Spanning Tree).
- Trees are always planar and hance can and should be drawn without any crossing edges.
- Two primary options for trees,
- Ranked embeddings, place the root at top, divide space into root-degree strips, remmove root, repeat recursively. Do some adjustments afterwards.
- Radial embeddings, useful for free trees, place root/center at the center of page, divide the space into angular sections based on the degree, repeat recursively. Adjust.
- Implementations : GraphViz.
- Related : Drawing graphs, planar drawings
Planarity Detection and Embedding
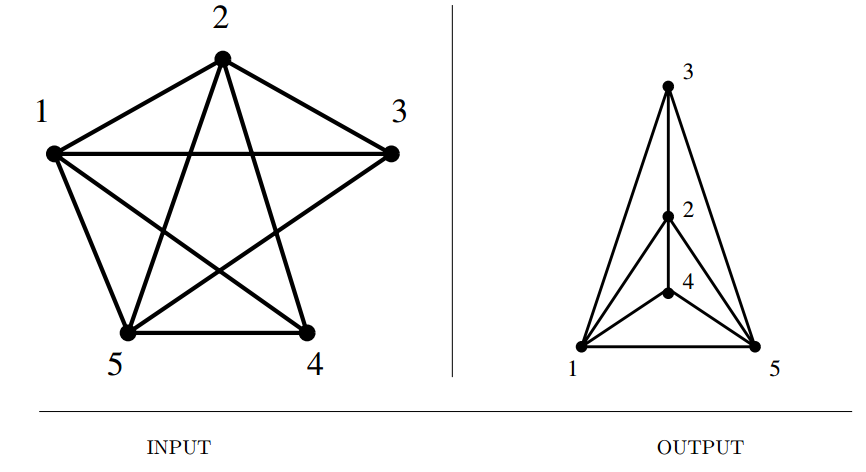
Input description: A graph \(G\).
Problem description: Can \(G\) be drawn in the plane such that no two edges cross?
If so, produce such a drawing.
- Planar drawings(or embeddings) make clear the structure of a given graph by eliminating crossing edges.
- However, not very much needed/encountered explicitly in applications.
- More important, planarity testing.
- Related : Graph partition, drawing trees
Comments
comments powered by Disqus