Contents:
Data Structures
Dictionaries
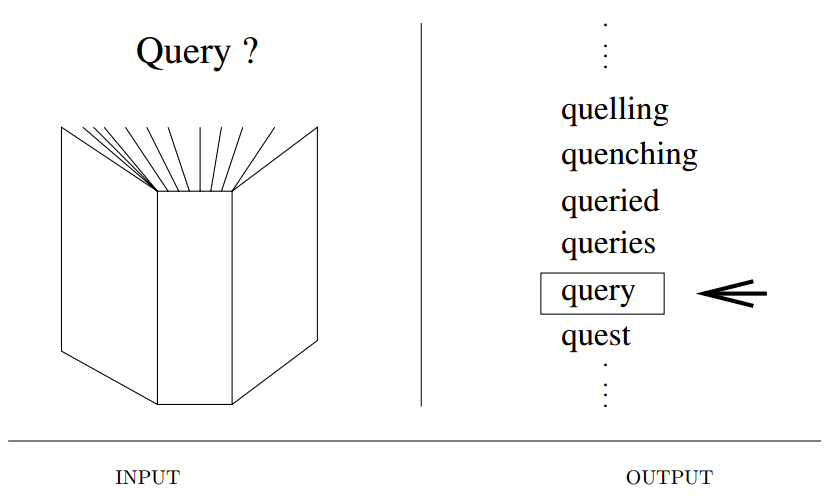
Input Description : A set of \(n\) records, each identified by one or more fields.
Problem description : Build and maintain a data structure to efficiently locate, insert, and delete the record associated with any query key \(q\).
- It is more important to avoid using a bad data structure than to identify the single best option available.
- Questions to ask:
- How many items will you have in your data structure?
- Do you know the relative frequencies of insert, delete, and search operations?
- Can we assume that the access pattern for keys will be uniform and random?
- Is it critical that individual operations be fast, or only that the total amount of work done over the entire program be minimized?
- Under the hood:
- Unsorted linked lists or arrays: For small data sets.
- Sorted linked lists or arrays
- Hash tables
- How do I deal with collisions? Open addressing or bucketing?
- How big should the table be? At least as big as \(m\), the number of items you expect to put in the table, it better be prime.
- What hash functions should I choose? For strings,
$$H(S,j) = \sum_{i=0}^{m-1}\alpha^{m-(i+1)}\times char(s_{i+j})\mod{m}$$\(\alpha\) is the size of the alphabet, \(char(x)\) maps a character to its ASCII code. This can be computer efficiently as,
$$H(S,j+1) = (H(S,j) - \alpha^{m-1}char(s_j))\alpha + s_{j+m}$$. In the end, make sure that the distribution is as uniform as possible.
- Binary search trees
- Elegant data structures that support fast insertions, deletions and queries.
- Do I need self balancing trees? Red-black trees, splay trees.
- Use the best implementations!!
- B-trees
- For data sets so large that they will not fit in the memory.
- Uses caches and secondary storage.
- Look for Cache-oblivious algorithms
- Skip lists
- Somewhat of a cult data structure.
- Implementations
- C++ :
std::map- Implemented as Binary Search Tree.
- LEDA
- hashing, perfect hashing, B-trees, red-black trees, random search trees, skip lists.
- Java Collections and Data Structures Library in Java
- C++ :
- Related : Sorting, searching
Priority Queues
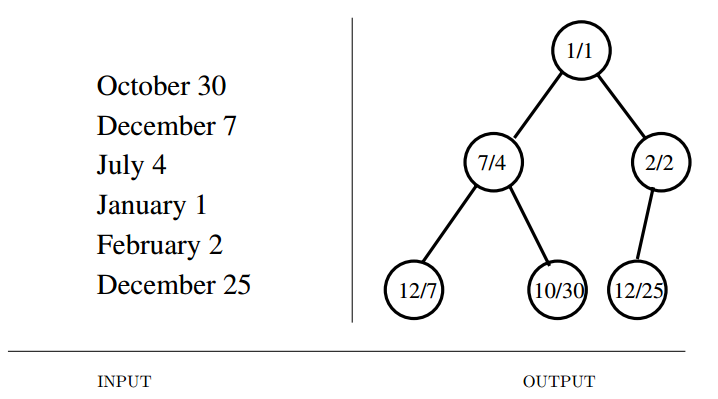
Input description: A set of records with numerically or otherwise totally-ordered keys.
Problem description: Build and maintain a data structure for providing quick access to the smallest or largest key in the set.
- Very useful in simulations(as future events ordered by time).
- Not required if insertions, deletions and queries are not intermixed.
- Questions to ask:
- What other operations do you need?
- Do you know the maximum data structure size in advance?
- Might you change the priority of the elements already in the queue?
- Choices:
- Sorted array or list
- Binary heaps
- Bounded height priority queue
- Useful for small, discrete range of keys.
- Binary Search trees
- Very useful when you need more dictionary operations or the size is unbounded.
- Fibonacci and pairing heaps
- Speed up decrease-key operation.
- Implementations
- C++ STL
std::priority_queue- Uses a
std::vectororstd::dequeue.
- Uses a
- LEDA
- Binary heaps, Fibonacci heaps, pairing heaps, Emde-Boas trees and bounded height priority queues
- Java Collections :
java.util.PriorityQueue
- C++ STL
- Related : Dictionaries, sorting, shortest path.
Suffix Trees and Arrays
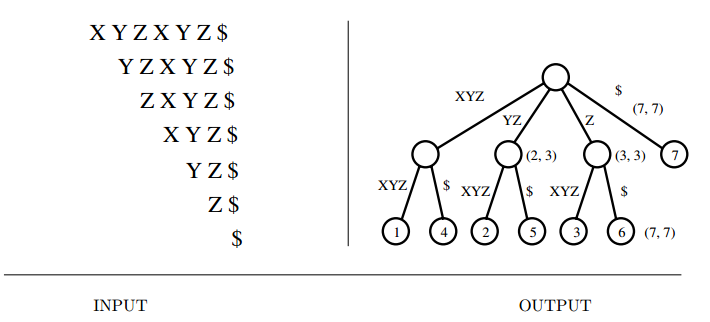
Input description: A reference string \(S\).
Problem description: Build a data structure to quickly find all places where an arbitrary query string \(q\) occurs in \(S\).
- Phenomenally useful for solving string problems.
- A suffix tree is simply a trie of all the proper suffixes of \(S\).
- Can be constructed in \(O(n)\) by making clever use of pointers!!
- What can you do with it?
- Find all occurrences of \(q\) as a substring of \(S\) in \(O(|q|+k)\), where \(k\) is the number of occurrences.
- Longest substring common to a set of strings.
- Find the longest palindrome in \(S\).
- They get even better when used as suffix arrays.
- Implementations
- C implementation by Schurmann and Stoye.
- Many C/C++ implementations in Pizza&Chili corpus
- Java
BioJava::SuffixTree
- Related : String Matching , Text Compression, Longest Common Substring
Graph Data Structures
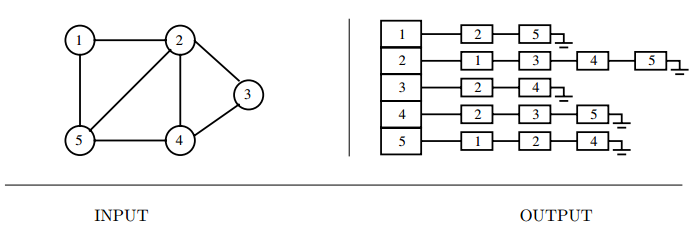
Input description: A graph \(G\).
Problem description: Represent the graph \(G\) using a flexible, efficient data structure.
- Adjacency matrices and adjacency lists.
- For most things, adjacency lists are the way to go, unless the graphs are very small or very dense.
- Questions to ask:
- How big will your graph be?
- How dense will your graph be?
- Which algorithms will you be implementing?
- Will you be modifying the graph over the course of your application?
- Prefer existing implementations.
- Graphs have different flavors, like Planar graphs, Hypergraphs, hierarchical graphs(representation).
- Implementation
- C++ : LEDA, Boost
- Java : JUNG, Data Structures Library(JDSL), JGraphT
- Stanford Graphbase
- Related : Set data structures, graph partition
Set data structures
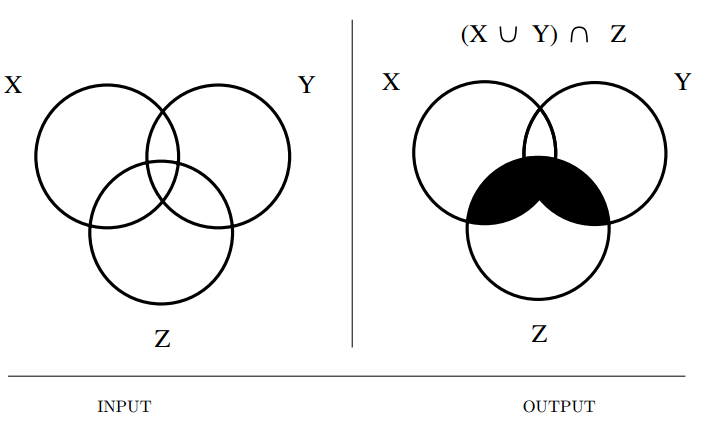
Input description: A universe of items \(U = \{u_1, \ldots , u_n}\\) on which is defined a collection of subsets \(S = \{S_1, \ldots , S_m\}\).
Problem description: Represent each subset so as to efficiently \((1)\) test whether \(u_i \in S_j\), \((2)\) compute the union or intersection of \(S_i\) and \(S_j\), and \((3)\) insert or delete members of \(S\).
- In mathematical terms, unordered collection of objects drawn from a fixed universal set.
- Uses a single canonical order for implementations, typically sorted.
- Distinguished from dictionaries(no fixed universal set) and strings(order is important).
- Multisets : An element can occur more than once.
- A system of subsets can also be represented as a hypergraph.
- Representations:
- Bit vectors : For a fixed universal set. Space efficient, fast intersection and union. Not very good for sparse subsets.
- Containers and dictionaries
- Bloom filters : Bit vectors with hashing.
- Set partition : When an item can be in only one set.
- Representations for set partition structures:
- Collection of containers : Membership testing is costly.
- Generalized bit vector : Union, intersection takes \(O(n),\; n = |U|\).
- Dictionary with a subset attribute : : Union, intersection are slow.
- Union-find data structures : Awesome asymptotic performance!!! Even better with path compression. Does not allow breaking subsets created by unions.
- Implementations
- C++ STL
setandmultiset. LEDA. - Java Collections
HashSetandTreeSet
- C++ STL
- Related : Generating subsets, generating partitions, set cover, minimum spanning tree.
Kd-Trees
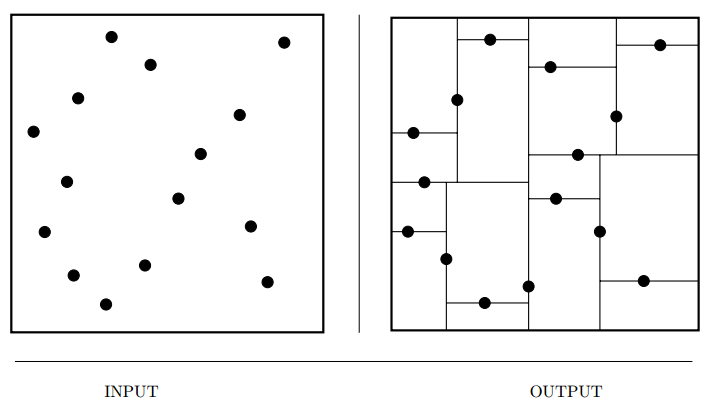
Input description: A set \(S\) of \(n\) points or more complicated geometric objects in \(k\) dimensions.
Problem description: Construct a tree that partitions space by half-planes such that each object is contained in its own box-shaped region.
- Spatial data structures that hierarchically decompose space into a small number of cells, each containing a few representatives from an input set of points.
- Flavors differ in how the splitting plane is selected:
- Cycling through the dimensions
- Cutting along the largest dimension
- Quadtrees or Octtrees : Cutting (axes-parallel planes) simultaneously along all the dimensions.
- BSP-trees : General(arbitrary) cutting planes to carve up cells. More complicated to work with.
- R-trees : Objects are partitioned into (possibly overlapping) boxes.
- Advantages :
- Point location.
- Nearest neighbor search.
- Range search
- Partial key search
- Effective upto say
20dimensions. - Implementations
- Related : Nearest-neighbor search, point location, range search.
Comments
comments powered by Disqus