Contents:
Numerical Problems
Check out Numerical Recipes
Whats different?
- Issues of Precision and Error. Floating point issues. Use both single and double precision, and think hard when they diverge.
- Extensive Libraries of Code. There is no reason to not to use all thats already written.
Solving Linear Equations
Input description: An \(m \times n\) matrix \(A\) and an \(m \times 1\) vector \(b\), together representing \(m\) linear equations on \(n\) variables.
Problem description: What is the vector \(x\) such that \(A \cdot x = b\)?
- Naive algorithm using Gaussian Elimination is \(O(n^3)\).
- Issues to worry about,
- Are roundoff errors and numerical stability affecting my solution? Use library routines.
- Which routine in the library should I use? Reduce to special form for faster implementations.
- Is my system sparse? Use specialized algorithms for faster implementations.
- Will I be solving many systems using the same coefficient matrix? Use LU Decomposition.
$$A \cdot x = (L \cdot U) \cdot x = L \cdot (U \cdot x) = b$$
This gives a solution in two \(O(n^2)\) since backsubstitution gives solves triangular system of equations in quadratic time instead of \(O(n^3)\), after \(LU\) decomposition has been done in \(O(n^3)\).
- Implementations
- LAPACK(C/C++)
- JScience, JAMA(Java)
- Related : Matrix multipplication, determinant/permanent
Bandwidth Reduction
Input description: A graph \(G = (V,E)\), representing an \(n \times n\) matrix \(M\) of zero and non-zero elements.
Problem description: Which permutation \(p\) of the vertices minimizes the length
of the longest edge when the vertices are ordered on a line—i.e. , minimizes
\(max(i,j) \in E |p(i) − p(j)|\)?
- Applied to matrices bandwidth reduction permutes the rows and columns of a sparse matrix to minimize the distance \(b\) of any non-zero entry from the center diagonal.
- Gaussian elimination can be performed in \(O(nb^2)\) on matrices of bandwidth \(b\). This is a big win over \(O(n^3)\) if \(b << n\).
- An example on graphs
- Arranging \(n\) circuit components in a line to minimize the length of the longest wire(and hence time delay) is a bandwidth problem.
- A hypertext application with links on a magnetic tape, we need to store linked objects near each other to minimize search time.
- More general formulations of rectangular circuit layouts and disks inherit the same hardness and heuristics.
- Variations
- In linear arrangement, we seek to minimize the sum of the lengths of the edges.
- In profile minimization, we seek to minimize the sum of one way distances for each vertex \(v\) the length of the longest edge whose other vertex is the left of \(v\).
- Unfortunately, this is NP-complete, even for a tree, thus or only options are a brute-force search or heuristics.
- Heuristic in worst case \(O(n^3)\), close to linear in practice.
- Brute-force in \(n!\) possible permutations.
- Implementations
- Del Corso and Manzini’s code for exact solutions to bandwidth problems.
- More references in the book.
- Related : Solving linear equations, topological sort
Matrix Multiplication
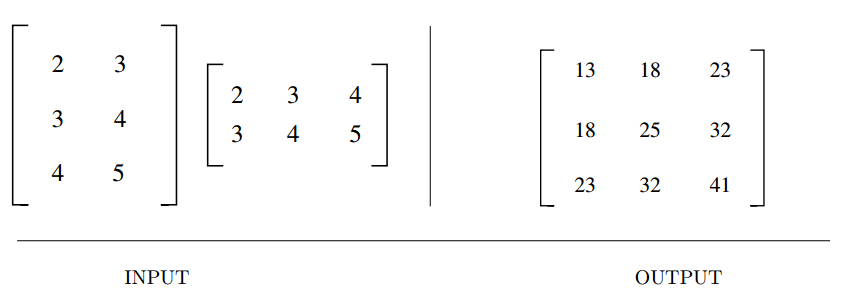
Input description: An \(x \times y\) matrix \(A\) and a \(y \times z\) matrix \(B\).
Problem description: Compute the \(x \times z\) matrix \(A \times B\).
- A fundamental problem in linear algebra.
- Multiplication can done in arbitrary order, with varying costs in \(O(xyz)\), but minimum can not be predicted.
- With bandwidth-\(b\) matrices, a speedup of \(O(xbz)\) can be achieved.
- Strassen's algorithm using divide-and-conquer runs in \(O(n^{2.81})\), but is only practically useful for \(n > 100\).
- For long chains on matrix multiplications, dynamic programming can be used to optimize the parenthesization to minimize the dimensions of intermediate results.
- Related : Solving linear equations, shortest path.
Determinants and Permanents
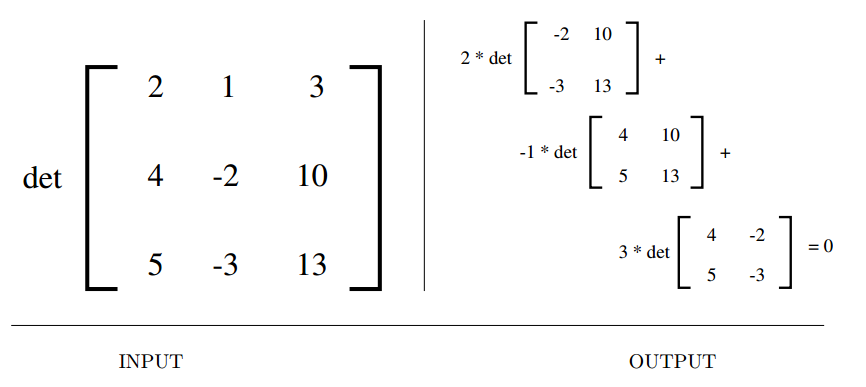
Input description: An \(n \times n\) matrix \(M\).
Problem description: What is the determinant \(|M|\) or permanent \(perm(M)\) of the matrix \(M\)?
- Used to solve a variety of problems.
- Testing if a matrix is singular, i.e. the matrix has no inverse, iff \(|M|=0\).
- Test whether a set of points lie in a plane, iff \(|M|=0\).
- Test whether a point lies in the left or right side of a line or a plane.
- Compute area or volume of a triangle, tetrahedron or other simplicial complex.
$$|M| = \sum_{i=1}^{n!}(-1)^{sign(\pi_i)} \prod_{j=1}^n M[j,\pi_j]$$
- This is \(O(n!)\). However can be done faster using LU decomposition in \(O(n^3)\).
- Closely related, permanent, counts the number of perfect matchings in \(G\), represented by its adjacency matrix \(M\).
$$perm(M) = \sum_{i=1}^{n!} \prod_{j=1}^n M[j, \pi_j] $$However, calculating this is NP-hard.
- Related : Solving linear equations, matching, geometric primitives.
Constrained and Unconstrained Optimization
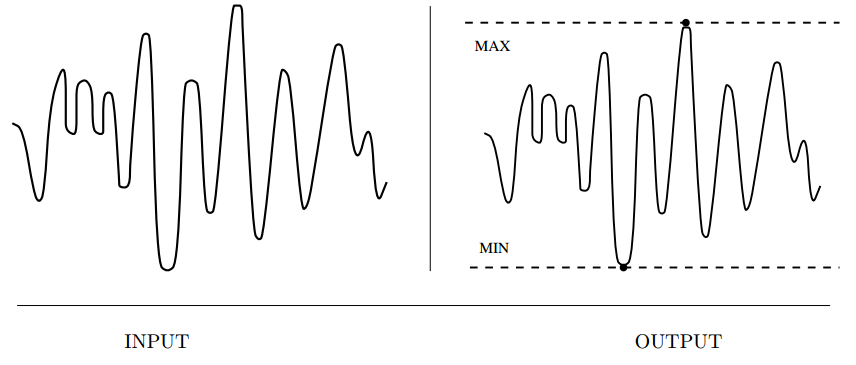
Input description: A function \(f(x_1, \ldots , x_n)\).
Problem description: What point \(p = (p_1, \ldots , p_n)\) maximizes (or minimizes) the
function \(f\)?
- Optimization arises whenever there is an objective function that must be tuned for optimal performance.
- Pattern recognition to energy/potential minimization
- Questions to ask,
- Am I doing constrained ot unconstrained optimization?
- Is the function I am trying to optimize described by a formula?
- Is it expensive to compute the function at a given point?
- How many dimensions do we have? How many do we need?
- How smooth is my function?
- Variations of gradient descent and simulated annealing
- Related : Linear programming, satisfiability
Linear Programming
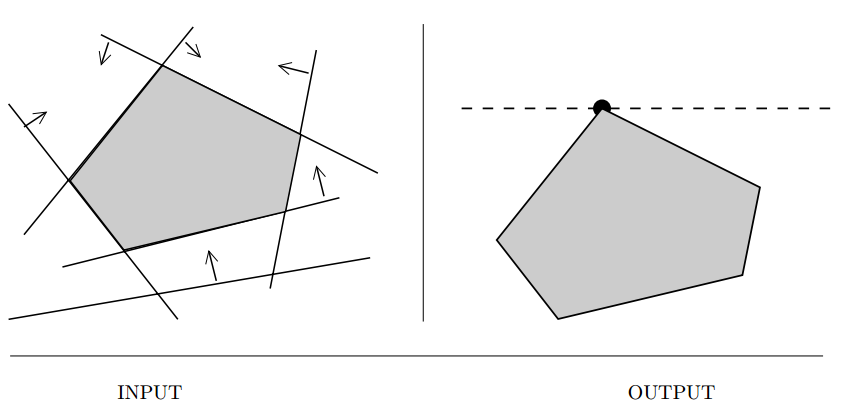
Input description: A set \(S\) of
S_i := \sum_{j=1}^m c_{ij} \cdot x_j \ge b_i, 1 \le i \le n\($
and a linear optimization function $f(X) = \sum_{j=1}^m c_j \cdot x_j\).
Problem description: Which variable assignment \(X'\) maximizes the objective function \(f\) while satisfying all inequalities \(S\)?
- Most important problem in mathematical optimization and operations research.
- Resource allocation
- Approximating the solution of inconsistent equations.
- Graph algorithms : Many can be solved using linear programming, most of the rest can be solved using Integer linear programming.
- The simplex method.
- While a simple algorithm, needs considerable art and the right data structures for large sparse systems.
- Also used, interior-point methods.
- Commercial solutions are of much higher quality than free/open source solutions.
- Questions to ask,
- Do any variables have integrality constraints? Although it is NP-complete, reasonable programs are available.
- Do I have more variables or constraints? If there are more constraints than variables, consider solving the dual LP, which would be much easier.
- What if my optimization function or constraints are not linear? Although fast implementations exist(for quadratic programming), but this is NP-complete.
- What if my model does not match the input format of my LP solver? Map your problem to standard forms.
- Implementations
- Related : Constrained and Unconstrained optimization, network flow
Random Number Generation
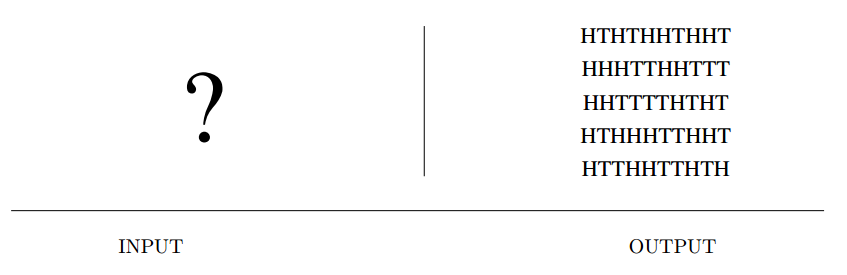
Input description: Nothing, or perhaps a seed.
Problem description: Generate a sequence of random integers.
- Discrete event simulations, passwords and cryptographic keys, randomized algorithms for graph and geometric problems.
Anyone who considers arithmetical methods of producing random digits is , of course, in a state of sin. -- Von Neumann.
- However, we can create pseudorandom numbers.
- Questions to ask,
- Should my program use the same random numbers each time it runs?
- How good is my compiler's built-in random number generator?
- What if I must implement my own random-number generator?
$$R_n = (aR_{n-1} + c) \mod m$$
- What if I don't want such large numbers?
- What if I need non-uniformly distributed random numbers?
- How long should I run my Monte-Carlo simulation to get the best results?
- Related : Constrained and unconstrained optimization, generating permutations, generating subsets, generating partitions.
Factoring and Primality Testing

Input description: An integer \(n\).
Problem description: Is \(n\) a prime number, and if not what are its factors?
- Long suspected of being only of mathematical interest, these problems have surprisingly many applications.
- The RSA, has tables, games.
- Several algorithms and implementations exist for generating and testing prime numbers and factoring(exponential).
- Related : Cryptography, high precision arithmetic
Arbitrary Precision Arithmetic
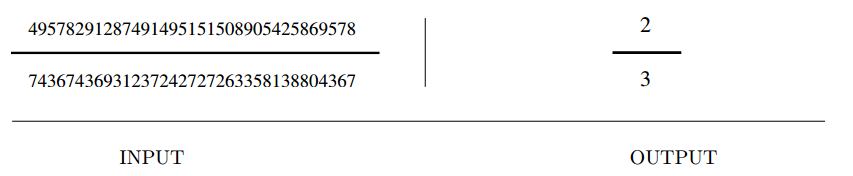
Input description: Two very large integers, \(x\) and \(y\).
Problem description: What is \(x + y\), \(x − y\), \(x \times y\), and \(x/y\)?
- Many applications require much larger integers than that can fit into a 32-bit integer.
- Questions to ask,
- Am I solving a problem instance requiring large integers, or do I have an embedded application?
- Do I need high- or arbitrary-precision arithmetic?
- What base should I do arithmetic in?
- How low-level are you willing to get for fast computation?
- The basic operations,
- Addition
- Subtraction
- Multiplication
- Division
- Exponentiation
- Related : Factoring Integers, cryptography
Knapsack Problem
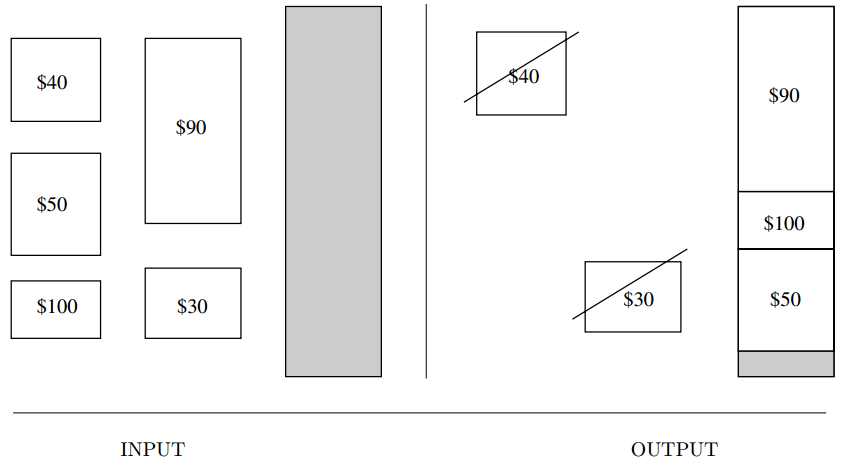
Input description: A set of items \(S = \{1, \cdots , n\}\), where item \(i\) has size \(s_i\) and value \(v_i\). A knapsack capacity is \(C\).
Problem description: Find the subset \(S' \subset S\) that maximizes the value of \(\sum_{i \in S'}v_i\), given that \(\sum_{i \in S'}s_i \le C\); i.e. , all the items fit in a knapsack of size \(C\).
- Resource allocation and financial constraints.
- Variations
- \(0/1\) problem, where objects can not be broken arbitarily. This makes it hard.
- Questions to consider,
- Does every item have the same cost/value or the same size? This becomes easy
- Does each item have the same “price per pound”? NP-complete, but still is considered "easy". Also called subset problem. Integer partition becomes a special case.
- Are all the sizes relatively small integers? Can be solved in \(O(nC)\), $C = $ capacity.
- What if I have multiple knapsacks? Bin-packing problem.
- Greedy heuristics often give "good" approximations.
- Based on 'price per pound'.
- Convert weights to integers using scaling.
- Related : Bin packing, integer programming
Discrete Fourier Transform

Input description: A sequence of \(n\) real or complex values \(h_i, 0 \le i \le n − 1\), sampled at uniform intervals from a function \(h\).
Problem description: The discrete Fourier transform \(H_m = \sum_{k=0}^{n-1} h_k e^{2\pi ikm/n\)} for \(0 \le m \le n − 1\).
- Electric engineers eat these for breakfast.
- They provide a way to transform samples of a time series into the frequency domain.
- Appplications include,
- Filtering
- Image compression
- Convolution and deconvolution
- Computing the correlation of functions
$$z(t) = \int_{-\inf}^{\inf}f(\tau)g(t + \tau)d\tau$$
- Naive implementation works in \(O(n^2)\).
- The fast Fourier transform(FFT) computes discrete fourier transform in \(O(n \log n)\).
- Often implemented in hardware for real time performance.
- Related : Data compression, high-precision arithmetic
Comments
comments powered by Disqus